Question

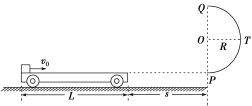
【题目】如图所示，虚线圆的半径为R，AC为光滑竖直杆，AB与BC构成直角的L形轨道，小球与AB、BC轨道间的动摩擦因数均为μ，A、B、C三点正好是圆上三点，而AC正好为该圆的直径，AB与AC的夹角为α.如果套在AC杆上的小球自A点静止释放，分别沿ABC轨道和AC直轨道运动，忽略小球滑过B处时的能量损耗.求：

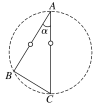
(1)小球在AB轨道上运动的加速度；

(2)小球沿ABC轨道运动到达C点时的速率；

(3)若AB、BC、AC轨道均光滑，如果沿ABC轨道运动到达C点的时间与沿AC直轨道运动到达C点的时间之比为5∶3，求α的正切值.

Answer 1

【答案】(1)gcosα－μgsinα (2)2 (3)2.4

【解析】(1)从A到B，由牛顿第二定律得：

mgcosα－μmgsinα＝ma

解得：a＝gcosα－μgsinα

(2)小球沿ABC轨道运动，从A到C，由动能定理可得：mv＝mg·2R－2μmg·2Rcosαsinα

解得：vC＝2

(3)设小球沿AC直导轨做自由落体运动，运动时间为t，则有：2R＝gt2

解得：t＝2

轨道均光滑，小球由A到B机械能守恒，设B点的速度为vB，则有：

mg·2Rcos2α＝mv

解得：vB＝2cosα

且依等时圆，tAB＝t，则B到C的时间为：

tBC＝t－t＝t＝

以后沿BC直导轨运动的加速度为：

a′＝gsinα，且BC＝2Rsinα

故2Rsinα＝vBtBC＋a′t

代入数据得：tanα＝2.4.