题目内容
5.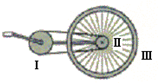 小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.如图是自行车的传动示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.当大齿轮Ⅰ(脚踏板)的转速通过测量为n(r/s)时,则大齿轮的角速度是2πnrad/s.若要知道在这种情况下自行车前进的速度,除需要测量大齿轮Ⅰ的半径r1,小齿轮Ⅱ的半径r2外,还需要测量的物理量是后轮半径r3(名称及符号).用上述物理量推导出自行车前进速度的表达式为:2πn$\frac{{r}_{3}{r}_{1}}{{r}_{2}}$.
小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度.他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度.如图是自行车的传动示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.当大齿轮Ⅰ(脚踏板)的转速通过测量为n(r/s)时,则大齿轮的角速度是2πnrad/s.若要知道在这种情况下自行车前进的速度,除需要测量大齿轮Ⅰ的半径r1,小齿轮Ⅱ的半径r2外,还需要测量的物理量是后轮半径r3(名称及符号).用上述物理量推导出自行车前进速度的表达式为:2πn$\frac{{r}_{3}{r}_{1}}{{r}_{2}}$.
分析 转速的单位为转/秒,即单位时间做圆周运动转过的圈数,转过一圈对应的圆心角为2π,所以角速度ω=转速n×2π,由于大齿轮I和小齿轮II是通过链条传动,所以大小齿轮边缘上线速度大小相等,又小齿轮II和车轮III是同轴转动,所以它们角速度相等,要知道车轮边缘线速度的大小,则需要知道车轮的半径;利用I和II线速度大小相等,II和III角速度相等,列式求III的线速度大小即可.
解答 解:转速为单位时间内转过的圈数,因为转动一圈,对圆心转的角度为2π,所以ω=$\frac{n×2π}{1}$rad/s=2πnrad/s,因为要测量自行车前进的速度,即车轮III边缘上的线速度的大小,根据题意知:轮I和轮II边缘上的线速度的大小相等,据v=Rω可知:r1ω1=r2ω2,已知ω1=2πn,则轮II的角速度ω2=$\frac{{r}_{1}}{{r}_{2}}$ω1.因为轮II和轮III共轴,所以转动的ω相等即ω3=ω2,根据v=Rω可知,要知道轮III边缘上的线速度大小,还需知道轮III的半径r3 ,其计算式v=r3ω3=$\frac{{r}_{3}{r}_{1}}{{r}_{2}}$2πn=2πn$\frac{{r}_{3}{r}_{1}}{{r}_{2}}$
故答案为:2πn,后轮半径r3,2πn$\frac{{r}_{3}{r}_{1}}{{r}_{2}}$.
点评 齿轮传动时,轮边缘上的线速度大小相等,同轴转动两轮的角速度相同;转速和角速度的互换问题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
15.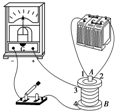 某学生将蓄电池、线圈A,线圈B、灵敏电流表G和开关,分别用导线连接成如图所示的实验电路,做观察电磁感应现象的实验.当他接通、断开开关时,发现灵敏电流表G的指针都没有偏转,已知所用器材完好,则其原因是( )
某学生将蓄电池、线圈A,线圈B、灵敏电流表G和开关,分别用导线连接成如图所示的实验电路,做观察电磁感应现象的实验.当他接通、断开开关时,发现灵敏电流表G的指针都没有偏转,已知所用器材完好,则其原因是( )
 某学生将蓄电池、线圈A,线圈B、灵敏电流表G和开关,分别用导线连接成如图所示的实验电路,做观察电磁感应现象的实验.当他接通、断开开关时,发现灵敏电流表G的指针都没有偏转,已知所用器材完好,则其原因是( )
某学生将蓄电池、线圈A,线圈B、灵敏电流表G和开关,分别用导线连接成如图所示的实验电路,做观察电磁感应现象的实验.当他接通、断开开关时,发现灵敏电流表G的指针都没有偏转,已知所用器材完好,则其原因是( )| A. | 电流表的正、负极接反 | B. | 线圈B的接头3、4接反 | ||
| C. | 蓄电池的正、负极接反 | D. | 开关位置接错 |
16.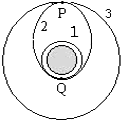 “神舟六号”飞行到第5圈时,在地面指挥控制中心的控制下,由近地点250km圆形轨道1经椭圆轨道2转变到远地点350km的圆轨道3.设轨道2与1相切于Q点,与轨道3相切于P点,如图所示,则飞船分别在1、2、3轨道上运行时( )
“神舟六号”飞行到第5圈时,在地面指挥控制中心的控制下,由近地点250km圆形轨道1经椭圆轨道2转变到远地点350km的圆轨道3.设轨道2与1相切于Q点,与轨道3相切于P点,如图所示,则飞船分别在1、2、3轨道上运行时( )
 “神舟六号”飞行到第5圈时,在地面指挥控制中心的控制下,由近地点250km圆形轨道1经椭圆轨道2转变到远地点350km的圆轨道3.设轨道2与1相切于Q点,与轨道3相切于P点,如图所示,则飞船分别在1、2、3轨道上运行时( )
“神舟六号”飞行到第5圈时,在地面指挥控制中心的控制下,由近地点250km圆形轨道1经椭圆轨道2转变到远地点350km的圆轨道3.设轨道2与1相切于Q点,与轨道3相切于P点,如图所示,则飞船分别在1、2、3轨道上运行时( )| A. | 飞船在轨道3上的速率大于在轨道1上的速率 | |
| B. | 飞船在轨道3上的角速度小于在轨道1上的角速度 | |
| C. | 飞船在轨道1上经过Q点时的加速度大于在轨道2上经过Q点的加速度 | |
| D. | 飞船在轨道2上经过P点时的加速度等于在轨道3上经过P点的加速度 |
13.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步.下列说法中正确的是( )
| A. | 开普勒通过对行星观测记录的研究发现了万有引力定律 | |
| B. | 卡文迪许测出了引力常量G的数值 | |
| C. | 牛顿三大运动定律均能进行实验验证 | |
| D. | 牛顿应用“理想斜面实验”推翻了亚里士多德的“力是维持物体运动的原因”的观点 |
20.对水下的潜水员,下列说法正确的是?( )
| A. | 由于全反射,看不到水面上的全部景像? | |
| B. | 潜水员看到岸边的树的位置和实际位置一样高? | |
| C. | 能看到水面上的全部景物? | |
| D. | 潜水员看到岸边的树的位置比实际位置偏低 |
17.某地地磁场磁感应强度大小为B=1.6×10-4T,与水平方向夹角53°,其在水平面内S=1.5m2的面积内地磁场的磁通量为( )
| A. | 1.44×10-4Wb | B. | 1.92×10-4Wb | C. | 1.92×10-5Wb | D. | 1.44×10-5Wb |
15.一只小船在静水中的速度为4m/s,要横渡宽为30m、水流速度为3m/s的河流,下述说法中正确的是( )
| A. | 此船不可能渡过此河 | B. | 此船不可能垂直到达正对岸 | ||
| C. | 此船过河的最短时间为6s | D. | 此船的合速度可能为6m/s |


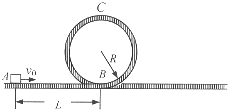 过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求:
过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求: