题目内容
9. 内壁光滑的圆槽半径为R,固定在竖直平面内,O点位圆心.一根长为$\sqrt{2}$R的轻杆,一端固定有质量为M的小球甲,另一端固定有质量为m的小球乙,将两小球放入圆槽内,小球乙位于圆槽的最低点,如图所示,轻杆由静止释放后( )
内壁光滑的圆槽半径为R,固定在竖直平面内,O点位圆心.一根长为$\sqrt{2}$R的轻杆,一端固定有质量为M的小球甲,另一端固定有质量为m的小球乙,将两小球放入圆槽内,小球乙位于圆槽的最低点,如图所示,轻杆由静止释放后( )| A. | 运动过程中甲乙两球速度大小始终相同 | |
| B. | 乙球一定能运动至右侧与圆心等高处 | |
| C. | 若M=m,则杆转过45°时甲球达最大速度 | |
| D. | 若M=$\sqrt{3}$m,则杆转过45°时甲球达最大速度 |
分析 两球沿杆方向的分速度始终相等,由速度的分解法分析它们速度关系.运用假设法分析乙球能否运动到右侧与圆心等高处.若M=m,整体的重心在杆的中点,整体的重力势能最小时,速度最大.甲与乙两小球系统,重力势能和动能相互转化,系统机械能守恒,由此分析.
解答 解:设甲乙两球速度大小分别为v甲和v乙.根据速度的分解有:v甲cos45°=v乙cos45°.则得 v甲=v乙.即运动过程中甲乙两球速度大小始终相同,故A正确.
B、取最低点所在水平面为参考平面.图示位置,甲乙组成的系统总机械能为 E1=MgR.
假设乙球能运动至右侧与圆心等高处,则此时系统的机械能为 E2=mgR.若m≠M,就违反了机械能守恒定律,所以乙球不一定能运动至右侧与圆心等高处.故B错误.
C、若M=m,整体的重心在杆的中点,当杆转过45°时整体的重力势能最小,由系统的机械能守恒可知,速度最大.故C正确.
D、若M=$\sqrt{3}$m,整体的重心不在杆的中点,应偏甲,所以杆转过的角度大于45°时整体的重力势能最小,速度最大.故D错误.
故选:AC
点评 本题的关键是抓住甲与乙两个球组成的系统机械能守恒,可以找出系统重心,分析重力势能的最小值,来确定动能的最大值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在研究下述运动时,能把物体看作质点的是( )
| A. | 研究地球的自转效应 | |
| B. | 向上抛出一枚硬币,研究落地时正面朝上的机会是多少 | |
| C. | 观看跳水比赛中的跳水运动员 | |
| D. | 卫星定位系统给大海里运动中的轮船定位 |
7.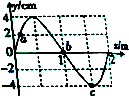 如图示为-列沿x轴正方向传播的简谐横波在t=0时刻的图象,振源周期为1s.以下说法正确的是( )
如图示为-列沿x轴正方向传播的简谐横波在t=0时刻的图象,振源周期为1s.以下说法正确的是( )
 如图示为-列沿x轴正方向传播的简谐横波在t=0时刻的图象,振源周期为1s.以下说法正确的是( )
如图示为-列沿x轴正方向传播的简谐横波在t=0时刻的图象,振源周期为1s.以下说法正确的是( )| A. | 质点b的振幅为0 | |
| B. | 质点a的振动方程为y=4sin(2πt+$\frac{5}{6}$π)cm | |
| C. | 从t=0时刻起,质点a比质点c先回到平衡位置 | |
| D. | 在t=0时刻,质点a、c所受的回复力大小之比为1:2 | |
| E. | 经过0.25s,质点b沿x轴正方向移动0.5m |
4.如图所示,用手握住锤子竖直向下做加速度大小为a的匀加速直线运动,则下列说法正确的是( )


| A. | 当a=g时,手给锤子的力为零 | |
| B. | 当a<g时,手给锤子的力竖直向下 | |
| C. | 当a>g时,手给锤子的力竖直向下 | |
| D. | 只要锤头未脱离锤柄,无论加速度多大,锤柄对锤头的力均为竖直向下 |
14.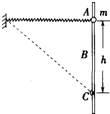 如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v0,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则( )
如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v0,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则( )
 如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v0,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则( )
如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v0,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则( )| A. | 圆环下滑过程中,加速度一直减小 | |
| B. | 圆环下滑过程中,克服摩擦力做的功为$\frac{1}{4}mv_0^2$ | |
| C. | 圆环在C处,弹簧的弹性势能为$mgh-\frac{1}{4}mv_0^2$ | |
| D. | 圆环上滑经过B的速度大于下滑经过B的速度 |
1.下列关于元电荷的说法正确的( )
| A. | 元电荷是除正、负电荷外的第三种电荷 | |
| B. | 元电荷就是质子 | |
| C. | 元电荷的电荷量e=1.6×10-19C | |
| D. | 物体所带的电荷量可以是任意值 |
18.一根粗细均匀的金属导线阻值为R,两端加上恒定电压U时,通过金属导线的电流强度为I,金属导线中自由电子定向移动的平均速率为v,若将金属导线均匀拉长,使其长度变为原来的2倍,仍给它两端加上恒定电压U,则下列说法正确的是( )
| A. | 此时金属导线的阻值为4R | |
| B. | 此时通过金属导线的电流为 $\frac{I}{4}$ | |
| C. | 此时自由电子定向移动的平均速率为 $\frac{v}{2}$ | |
| D. | 此时自由电子定向移动的平均速率为 $\frac{v}{4}$ |
19.下列关于自由落体运动的说法中正确的是( )
| A. | 物体在地球表面附近做自由落体运动过程中,每秒速度增加约为9.8m/s | |
| B. | 自由落体运动是一种匀速运动 | |
| C. | 各地的重力加速度都一样大 | |
| D. | 物体越重,下落得越快 |
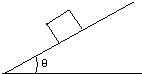 如图所示,一质量为m的物体放在倾角为θ的斜面上.
如图所示,一质量为m的物体放在倾角为θ的斜面上.