题目内容
(20分)如图(a)所示,两块足够大的平行金属板竖直放置,板间加有匀强电场和磁场,电场和磁场的大小随时间按图(b)和图(c)所示的规律变化(规定垂直于纸面向外为磁感应强度的正方向)。在t=0时,由负极板内侧释放一初速度为零的带负电粒子,粒子的重力不计。在t=37t0/12时,带电粒子被正极板吸收。已知电场强度E0、粒子的比荷q/m以及t0。而磁感应强度B1、B2(均未知)的比值为1﹕3,在t0~2t0时间内,粒子在磁场中做匀速圆周运动的周期为t0。求:
(1)当带电粒子离负极板的距离S0="q" E0t02/2m时,粒子在两极板间运动的时间;
(2)两平行板间的距离d 。


(1)当带电粒子离负极板的距离S0="q" E0t02/2m时,粒子在两极板间运动的时间;
(2)两平行板间的距离d 。



(1) 对应的时刻为:t0、3t0/2、2t0(2)d = 2E0qt02/m + E0qt02/3лm
解:(1)由牛顿第二定律及运动学公式:

E0q =" ma " …… (2分)
S1 = at02/2 …… (2分)
S1 = E0qt02/2m
∵ S1 = S0
∴如图:当 S1 = S0 = E0qt02/2m时,
对应的时刻为:t0、3t0/2、2t0 .(3分)
(2)由粒子的运动情况,前3t0时间内,粒子匀加速的时间为2t0,做圆周运动时间为t0,则粒子匀加速直线运动的位移
S = a(2t0)2/2 = 4S0 …… (2分)
最后t0/12粒子做圆周运动,设粒子的速度为v2,
V2 = 2at0 …… (1分)
设粒子在磁场B2中的轨道半径为R2,
B2v2q = mv22/R2 …… (2分)
粒子在B1磁场中运动的周期T1 = 2лm/qB1 = t0…… (2分)
解得:R2 = E0qt02/3лm …… (1分)
∵粒子在B2中的周期:T2 = 2лm/qB2 = t0/3 …… (2分)
∴t0/12时间内粒子转过的角度θ=л/2 …… (1分)
即:d = S+R2…… (1分)
解得:d = 2E0qt02/m + E0qt02/3лm …… (1分)

E0q =" ma " …… (2分)
S1 = at02/2 …… (2分)
S1 = E0qt02/2m
∵ S1 = S0
∴如图:当 S1 = S0 = E0qt02/2m时,
对应的时刻为:t0、3t0/2、2t0 .(3分)
(2)由粒子的运动情况,前3t0时间内,粒子匀加速的时间为2t0,做圆周运动时间为t0,则粒子匀加速直线运动的位移
S = a(2t0)2/2 = 4S0 …… (2分)
最后t0/12粒子做圆周运动,设粒子的速度为v2,
V2 = 2at0 …… (1分)
设粒子在磁场B2中的轨道半径为R2,
B2v2q = mv22/R2 …… (2分)
粒子在B1磁场中运动的周期T1 = 2лm/qB1 = t0…… (2分)
解得:R2 = E0qt02/3лm …… (1分)
∵粒子在B2中的周期:T2 = 2лm/qB2 = t0/3 …… (2分)
∴t0/12时间内粒子转过的角度θ=л/2 …… (1分)
即:d = S+R2…… (1分)
解得:d = 2E0qt02/m + E0qt02/3лm …… (1分)

练习册系列答案
相关题目
 ,方向垂直纸面向里。现有一质量为m、带电量为q的带正电粒子,从O点沿图示方向进入
,方向垂直纸面向里。现有一质量为m、带电量为q的带正电粒子,从O点沿图示方向进入 中。
中。
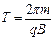 。
。
 ,宽为
,宽为 的虚线区域内有垂直纸面的匀强磁场B。现有一初速度为零、带电量为q、质量为m的离子(不计重力)从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从NF边界上某点垂直于虚线边界射出。求:
的虚线区域内有垂直纸面的匀强磁场B。现有一初速度为零、带电量为q、质量为m的离子(不计重力)从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从NF边界上某点垂直于虚线边界射出。求:
 ,今在两板正中央
,今在两板正中央 处放一电荷
处放一电荷 ,则它受到的电场力大小为( )
,则它受到的电场力大小为( )





 极板P、Q、M、N各带什么电荷?
极板P、Q、M、N各带什么电荷? 。则电子进入电容器MN时距MN中心线的距离?要让电子通过电容器MN后又能回到O点,还需在电容器左侧区域加一个怎样的匀强磁场?
。则电子进入电容器MN时距MN中心线的距离?要让电子通过电容器MN后又能回到O点,还需在电容器左侧区域加一个怎样的匀强磁场? (重力不计)。试求:(1)带电粒子进入磁场时速度的大小?
(重力不计)。试求:(1)带电粒子进入磁场时速度的大小?
