题目内容
上端开口的圆柱形气缸竖直放置，截面积为0.2米2的活塞将一定质量的气体和一形状不规则的固体A封闭在气缸内．温度为 300K时，活塞离气缸底部的高度为0.6米；将气体加热到330K时，活塞上升了0.05米，不计摩擦力及固体体积的变化．求物体A的体积．分析：加热活塞上升时，气缸内气体发生等压变化．根据盖-吕萨克定律列方程求解物体A的体积．
解答：解：设A的体积为V，T1=300K，T2=330K，S=0.2m2，h=0.6m
h2=0.6m+0.05m=0.65m ①
气体发生等压变化，根据盖-吕萨克定律
=
②
（h1S-V）T2=（h2S-V）T1
故V=
S=0.02m3．
答：A的体积为0.02m3．
h2=0.6m+0.05m=0.65m ①
气体发生等压变化，根据盖-吕萨克定律
| h2S-V |
| T2 |
| h1S-V |
| T1 |
（h1S-V）T2=（h2S-V）T1
故V=
| h1T2-h2T1 |
| T2-T1 |
答：A的体积为0.02m3．
点评：本题关键是判断出气体发生的是等压变化．封闭气体的压强可以以活塞为研究对象根据平衡条件列方程来分析．
练习册系列答案
相关题目
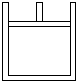如图，上端开口的圆柱形气缸竖直放置，截面积为5×10-3m2．一定质量的气体被质量为2.0kg的光滑活塞封闭在气缸内，其压强为
，一定质量的气体被质量为2.0kg的光滑活塞封闭在气缸内，其压强为____pa（大气压强取1.01*
，g取
）。若从初温
开始加热气体，使活塞离气缸底部的高度由0.5m缓慢变为0.51m，则此时气体的温度为____℃。
，一定质量的气体被质量为2.0kg的光滑活塞封闭在气缸内，其压强为____pa（大气压强取1.01*
，g取
）。若从初温
开始加热气体，使活塞离气缸底部的高度由0.5m缓慢变为0.51m，则此时气体的温度为____℃。
如图，上端开口的圆柱形气缸竖直放置，截面积为5´10－3m2.一定质量的气体被质量为2.0kg的光滑活塞封闭在气缸内，其压强为_________Pa（大气压强取1.01´105Pa，g取10m/s2）。若从初温27°C开始加热气体，使活塞离气缸底部的高度由0.50m缓慢地变为0.51m。则此时气体的温度为_________°C。