题目内容
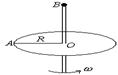
如右图所示,半径为r、圆心为O1的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一对竖直放置的平行金属板M和N,两板间距离为L,在MN板中央有一个小孔O2、O3,O1、O2、O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距也为L的足够长光滑金属导轨,导体棒PQ与导轨接触良好,与电阻为R的电阻形成闭合回路(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中。有一束电荷量为+q、质量为m的粒子流(重力不计),以速率v0从圆形磁场边界上的最低点E沿半径方向射入圆形磁场区域,最后从小孔O3射出。现释放导体棒PQ,其下滑h后开始匀速运动,此后粒子恰好不能从O3射出,而从圆形磁场的最高点F射出。求:
(1)圆形磁场的磁感应强度B′;
(2)导体棒的质量M;
(3)棒下落h的整个过程中,电阻上产生的电热;
(4)粒子从E点到F点所用的时间。
解:(1)在圆形磁场中做匀速圆周运动,洛伦磁力提供向心力qv0B′=m·![]() ;①
;①
得B′=![]() 。②
。②
(2)根据题意粒子恰好不能从O3射出的条件为![]() mv02=qUPQ③
mv02=qUPQ③
PQ棒匀速运动时,Mg=B·![]() ·L,④
·L,④
由③④得M=![]() v 02。⑤
v 02。⑤
(3)导体棒匀速运动时,速度大小为vm,UPQ=BLvm⑥
代入③中得vm=![]() ,⑦
,⑦
由能量守恒:QR=Mgh-![]() Mvm2,
Mvm2,
解得
QR=![]() v02-
v02-![]() 。⑧
。⑧
(4)在圆形磁场内的运动时间为t1,
t1=![]() +
+![]() =
=![]() ·
·![]() 。⑨
。⑨
在电场中往返运动的时间为t2;
由L=![]() ,⑩
,⑩
t2=![]() ,
,![]()
故t=t1+t2=![]() 0。
0。![]()

练习册系列答案
相关题目