题目内容
14.太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动,当地球恰好运行到某地外行星和太阳之间,且三者几乎排成一条直线的现象,天文学称为“行星冲日”.据报道,2014年各行星冲日时间分别是:l月6日木星冲日;4月9日火星冲日,5月11 日土星冲日;8月29日海王星冲日;10月8日天王星冲日.已知地球及各地外行星绕太阳运动的轨道半径如下表所示,其中$\sqrt{5.2}$=2.28,则下一次木星冲日会发生在( )| 地球 | 火星 | 木星 | 土星 | 天王星 | 海王星 | |
| 轨道半径(AU) | 1.0 | 1.5 | 5.2 | 9.5 | 19 | 30 |
| A. | 2015年上半年 | B. | 2015年下半年 | C. | 2016年上半年 | D. | 2016年下半年 |
分析 行星围绕太阳做匀速圆周运动,根据开普勒第三定律,其轨道半径的三次方与周期T的平方的比值都相等求出木星的周期;抓住地球转动的角度比木星转动的角度多2π,求出下一次木星冲日会发生的时间.
解答 解:根据开普勒第三定律,有:$\frac{{R}^{3}}{{T}^{2}}=\frac{{{R}_{地}}^{3}}{{{T}_{地}}^{2}}$,代入数据解得木星的周期 T=$\sqrt{5.{2}^{3}}$=11.86年,
2014年1月6日木星冲日,木星的公转周期为11.86年,根据$\frac{2π}{{T}_{地}}t-\frac{2π}{T}t=2π$,解得t≈1.1年,即经过1.1年再一次出现木星冲日,可知下一次木星冲日在2015年的上半年.故A正确,B、C、D错误.
故选:A.
点评 本题关键是结合开普勒第三定律分析(也可以运用万有引力等于向心力列式推导出),知道相邻的两次行星冲日的时间中地球多转动一周.

练习册系列答案
相关题目
6.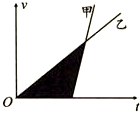 甲、乙两物体沿同一直线同方向运动,如图所示为两物体运动的v-t图象,阴影部分的面积S0,两物体出发点间距S(S>S0),则下列说法正确的是( )
甲、乙两物体沿同一直线同方向运动,如图所示为两物体运动的v-t图象,阴影部分的面积S0,两物体出发点间距S(S>S0),则下列说法正确的是( )
 甲、乙两物体沿同一直线同方向运动,如图所示为两物体运动的v-t图象,阴影部分的面积S0,两物体出发点间距S(S>S0),则下列说法正确的是( )
甲、乙两物体沿同一直线同方向运动,如图所示为两物体运动的v-t图象,阴影部分的面积S0,两物体出发点间距S(S>S0),则下列说法正确的是( )| A. | 若乙在前甲在后,两物体相遇前的最大距离为S+S0 | |
| B. | 若乙在前甲在后,两物体相遇前的最大距离为S-S0 | |
| C. | 若甲在前乙在后,两物体间的最小距离为S+S0 | |
| D. | 若甲在前乙在后,两物体间的最小距离为S-S0 |
5.两个分别带有电荷量-Q和+3Q的相同金属小球(均可视为点电荷),固定在相距为r的两处,它们间库仑力的大小为F,两小球相互接触后将其固定距离变为$\frac{r}{2}$,则两球间库仑力的大小为( )
| A. | $\frac{3}{4}$F,排斥力 | B. | $\frac{3}{4}$F,吸引力 | C. | $\frac{4}{3}$F,排斥力 | D. | $\frac{4}{3}$F,吸引力 |
2.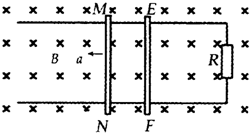 如图所示,相距为L的两条足够长的平行金属导轨右端连接有一定值电阻R,整个装置被固定在水平地面上,整个空间存在垂直于导轨平面向下的匀强磁场,磁感应强度大小为B,两根质量均为m,电阻都为R,与导轨间的动摩擦因数都为μ的相同金属棒MN、EF垂直放在导轨上.现在给金属棒MN施加一水平向左的作用力F,使金属棒MN从静止开始以加速度a做匀加速直线运动,若重力加速度为g,导轨电阻不计,最大静摩擦力与滑动摩擦力相等.则下列说法正确的是( )
如图所示,相距为L的两条足够长的平行金属导轨右端连接有一定值电阻R,整个装置被固定在水平地面上,整个空间存在垂直于导轨平面向下的匀强磁场,磁感应强度大小为B,两根质量均为m,电阻都为R,与导轨间的动摩擦因数都为μ的相同金属棒MN、EF垂直放在导轨上.现在给金属棒MN施加一水平向左的作用力F,使金属棒MN从静止开始以加速度a做匀加速直线运动,若重力加速度为g,导轨电阻不计,最大静摩擦力与滑动摩擦力相等.则下列说法正确的是( )
 如图所示,相距为L的两条足够长的平行金属导轨右端连接有一定值电阻R,整个装置被固定在水平地面上,整个空间存在垂直于导轨平面向下的匀强磁场,磁感应强度大小为B,两根质量均为m,电阻都为R,与导轨间的动摩擦因数都为μ的相同金属棒MN、EF垂直放在导轨上.现在给金属棒MN施加一水平向左的作用力F,使金属棒MN从静止开始以加速度a做匀加速直线运动,若重力加速度为g,导轨电阻不计,最大静摩擦力与滑动摩擦力相等.则下列说法正确的是( )
如图所示,相距为L的两条足够长的平行金属导轨右端连接有一定值电阻R,整个装置被固定在水平地面上,整个空间存在垂直于导轨平面向下的匀强磁场,磁感应强度大小为B,两根质量均为m,电阻都为R,与导轨间的动摩擦因数都为μ的相同金属棒MN、EF垂直放在导轨上.现在给金属棒MN施加一水平向左的作用力F,使金属棒MN从静止开始以加速度a做匀加速直线运动,若重力加速度为g,导轨电阻不计,最大静摩擦力与滑动摩擦力相等.则下列说法正确的是( )| A. | 从金属棒MN开始运动到金属棒EF开始运动经历的时间为t=$\frac{3μmgR}{{{B^2}{L^2}a}}$ | |
| B. | 若从金属棒MN开始运动到金属棒EF开始运动经历的时间为T,则此过程中流过电阻R的电荷量为q=$\frac{{BLa{T^2}}}{6R}$ | |
| C. | 若从金属棒MN开始运动到金属棒EF开始运动经历的时间为T,则金属棒EF开始运动时,水平拉力F的瞬时功率为P=(ma+μmg)aT | |
| D. | 从金属棒MN开始运动到金属棒EF开始运动的过程中,两金属棒的发热量相等 |
9.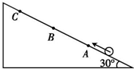 如图所示,一小球以某一速度从倾角为30°的光滑斜面底端冲向顶端,然后又返回底端.A、B、C是斜面上的三个点,其中C为小球到达的最高点,B是AC段的中点.若小球在A、C间往返的总时间为t,那么小球经过B点时速度的大小等于( )
如图所示,一小球以某一速度从倾角为30°的光滑斜面底端冲向顶端,然后又返回底端.A、B、C是斜面上的三个点,其中C为小球到达的最高点,B是AC段的中点.若小球在A、C间往返的总时间为t,那么小球经过B点时速度的大小等于( )
 如图所示,一小球以某一速度从倾角为30°的光滑斜面底端冲向顶端,然后又返回底端.A、B、C是斜面上的三个点,其中C为小球到达的最高点,B是AC段的中点.若小球在A、C间往返的总时间为t,那么小球经过B点时速度的大小等于( )
如图所示,一小球以某一速度从倾角为30°的光滑斜面底端冲向顶端,然后又返回底端.A、B、C是斜面上的三个点,其中C为小球到达的最高点,B是AC段的中点.若小球在A、C间往返的总时间为t,那么小球经过B点时速度的大小等于( )| A. | $\frac{\sqrt{2}}{2}$gt | B. | $\frac{\sqrt{2}}{4}$gt | C. | $\frac{\sqrt{2}}{8}$gt | D. | $\frac{\sqrt{2}}{16}$gt |
19.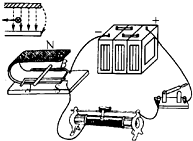 观察实验.选出正确答案,在如图所示的实验装置中,接通电源,导体AB受磁场力的作用而发生运动,然后改变电流方向或磁感线方向.则( )
观察实验.选出正确答案,在如图所示的实验装置中,接通电源,导体AB受磁场力的作用而发生运动,然后改变电流方向或磁感线方向.则( )
 观察实验.选出正确答案,在如图所示的实验装置中,接通电源,导体AB受磁场力的作用而发生运动,然后改变电流方向或磁感线方向.则( )
观察实验.选出正确答案,在如图所示的实验装置中,接通电源,导体AB受磁场力的作用而发生运动,然后改变电流方向或磁感线方向.则( )| A. | 在上述实验现象中,是机械能转化为电能 | |
| B. | 改变电流方向,通电导体所受磁场力的方向不变 | |
| C. | 改变磁感线方向(磁铁N、S极对调)通电导体所受 磁场力的方向不变 | |
| D. | 同时改变电流和磁感线的方向(磁铁N、S极对调),通电导体所受磁场力方向不变 |
6. 某同学探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…挂七个50g的砝码时,指针指示的刻度数值记作L7.
某同学探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…挂七个50g的砝码时,指针指示的刻度数值记作L7.
(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.测量记录表:
(2)实验中,L3和L7两个值还没有测定,请你根据如图将这两个测量值填入记录表中.
(3)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:
d1=L4-L0=6.90cm;d2=L5-L1=6.90cm; d3=L6-L2=7.00cm;
请你给第四个差值:d4=L7-L3=7.20cm.
(4)根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{4×4}$,代入数据解得△L=1.75cm.
(5)计算弹簧的劲度系数k=28.0N/m.(g取9.8m/s2)
 某同学探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…挂七个50g的砝码时,指针指示的刻度数值记作L7.
某同学探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…挂七个50g的砝码时,指针指示的刻度数值记作L7.(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.测量记录表:
| 代表 符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
(3)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:
d1=L4-L0=6.90cm;d2=L5-L1=6.90cm; d3=L6-L2=7.00cm;
请你给第四个差值:d4=L7-L3=7.20cm.
(4)根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{4×4}$,代入数据解得△L=1.75cm.
(5)计算弹簧的劲度系数k=28.0N/m.(g取9.8m/s2)
4.物体受到几个外力的作用而作匀速直线运动,如果撤掉其中的一个力,它可能做( )
| A. | 匀速直线运动 | B. | 匀变速直线运动 | C. | 匀速圆周运动 | D. | 类平抛运动 |