Question

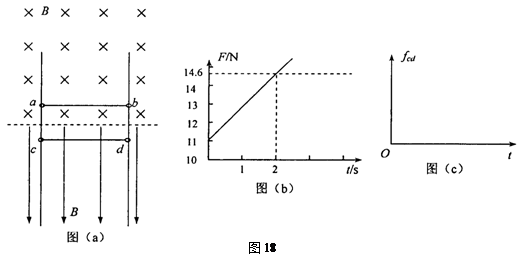
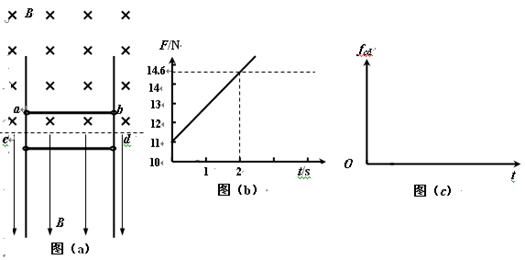
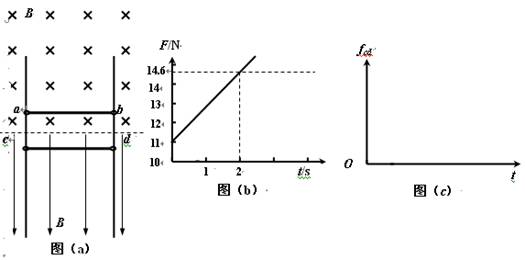
相距L＝1.5m的足够长金属导轨竖直放置，质量为m1＝1.0kg的金属棒ab和质量为m2＝0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同。ab棒光滑，cd棒与导轨间动摩擦因数为μ＝0.75，两棒总电阻为R=1.8Ω，导轨电阻不计。ab棒在方向竖直向上，大小按图（b）所示规律变化的外力F作用下，从静止开始，沿导轨匀加速运动，同时cd棒也由静止释放。取重力加速度g=10m/s2。

（1）求出磁感应强度B的大小和ab棒加速度大小；
（2）已知在2 s内外力F做功40 J，求这一过程中两金属棒产生的总焦耳热；
（3）判断cd棒将做怎样的运动，求出cd棒达到最大速度所需的时间t0，并在图（c）中定性画出cd棒所受摩擦力fcd随时间变化的图象。               

Answer 1

(1) 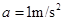，B＝1.2T；(2)18J；(3)2s，如答图。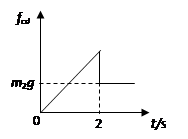

解析考点：导体切割磁感线时的感应电动势；牛顿第二定律；动能定理的应用；能量守恒定律．
分析：（1）由E=BLv、I= 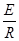、F=BIL、v=at，及牛顿第二定律得到F与时间t的关系式，再根据数学知识研究图象（b）斜率和截距的意义，即可求磁感应强度B的大小和ab棒加速度大小．
（2）由运动学公式求出2s末金属棒ab的速率和位移，根据动能定理求出两金属棒产生的总焦耳热．
（3）分析cd棒的运动情况：cd棒先做加速度逐渐减小的加速运动，当cd棒所受重力与滑动摩擦力相等时，速度达到最大；然后做加速度逐渐增大的减速运动，最后停止运动．
cd棒达到最大速度时重力与摩擦力平衡，而cd棒对导轨的压力等于安培力，可求出电路中的电流，再由E=BLv、欧姆定律求出最大速度．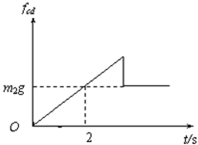

解（1）经过时间t，金属棒ab的速率 v="at"
此时，回路中的感应电流为 I==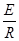
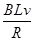
对金属棒ab，由牛顿第二定律得 F-BIL-m₁g=m₁a
由以上各式整理得：F=m₁a+m₁g+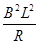at
在图线上取两点：t₁=0，F₁=11N； t₂=2s，F₂=14.6N
代入上式得 a=1m/s²，B="1.2T"
（2）在2s末金属棒ab的速率 v_t="at=2m/s"
所发生的位移 S=at²=2m
由动能定律得 W_F-m₁gS-W_安=m₁v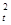
又 Q=W_安
联立以上方程，解得
Q=W_F-mgs-m v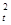=40-1×10×2-×1×2²=18（J）
（3）cd棒先做加速度逐渐减小的加速运动，当cd棒所受重力与滑动摩擦力相等时，速度达到最大；然后做加速度逐渐增大的减速运动，最后停止运动．
当cd棒速度达到最大时，对cd棒有：m₂g=μF_N
又 F_N=F_安 F_安=BIL
整理解得 m₂g=μBIL
对abcd回路：I==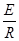
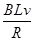
解得 v_m=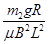="2m/s"
v_m=at₀得 t₀=2s
f_cd随时间变化的图象如图所示．
答：
（1）求出磁感应强度B的大小为1.2T，ab棒加速度大小1m/s²；
（2）这一过程中两金属棒产生的总焦耳热是18J；
（3）cd棒达到最大速度所需的时间t₀为2s，cd棒所受摩擦力f_cd随时间变化的情况如图．