题目内容
如图所示，不计滑轮和绳的质量及一切摩擦阻力，已知MB=3kg，要使物体C有可能处于平衡状态，那么Mc的可能值为（ ）分析：当mA＞＞mB时和当mA=0时，讨论绳子中的拉力，得出C的质量的取值范围．
解答：解：对AB整体用牛顿第二定律分析：
（mA-mB）g=（mA+mB）a
a=
g
当mA＞＞mB时，a=g．
对B隔离用牛顿第二定律分析：
T-mB=mBa
所以T=2mBg
即当mA＞＞mB时，AB之间的绳的最大拉力为2mBg，所以在C这边的拉力为4mB，为12Kg，这是最大值．
当mA=0时，B这边绳的拉力为0，C那边的拉力也为0，这是最小值．
所以AB符合．
故选AB．
（mA-mB）g=（mA+mB）a
a=
| mA-mB |
| mA+mB |
当mA＞＞mB时，a=g．
对B隔离用牛顿第二定律分析：
T-mB=mBa
所以T=2mBg
即当mA＞＞mB时，AB之间的绳的最大拉力为2mBg，所以在C这边的拉力为4mB，为12Kg，这是最大值．
当mA=0时，B这边绳的拉力为0，C那边的拉力也为0，这是最小值．
所以AB符合．
故选AB．
点评：此题的关键是当mA＞＞mB时，绳子中的最大拉力，从而可知C的最大质量．此题有一定的难度，属于中档题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
m2 B.m1＞
m2
m2 D.m1一定小于m2
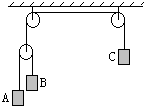
如图所示，不计滑轮和绳的质量及一切摩擦阻力，已知MB=3kg，要使物体C有可能处于平衡状态，那么Mc的可能值为
如图所示，不计滑轮和绳的质量及一切摩擦阻力，已知MB=3kg，要使物体C有可能处于平衡状态，那么Mc的可能值为（ ）