Question

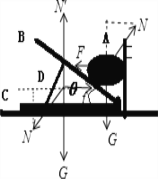
【题目】如图所示，有一个光滑圆柱体A夹在平板B与竖直墙壁之间，平板通过铰链与底座C相连，底座左端与液压器D相连.通过调节液压器的高度可以改变平板与底座之间的夹角θ. A的重力为G， B、C及D的总重力也为G.底座C与水平地面间的动摩擦因数为μ（0.5＜μ＜1），最大静摩擦力等于滑动摩擦力.则下列说法正确的是（　　）

A. C与地面间的摩擦力总等于2μG

B. θ角增大时，地面对C的摩擦力一直在增大

C. 要保持底座C静止不动，应满足tanθ2μ

D. 若保持θ=45°不变，圆柱体的重力增大△G，仍要保持底座C静止，则△G的最大值为

Answer 1

【答案】CD

【解析】对A进行受力分析，如图所示，根据平衡条件得： 解得： ，对B、C及D整体进行受力分析，如图所示，

当B、C及D整体静止时，摩擦力f=Nsinθ=Gtanθ，当θ角增大时，地面对C的摩擦力增大，当摩擦力超过最大静摩擦力后，变为滑动摩擦力，此时f滑=2μG，故AB错误；要保持底座C静止不动，则f≤f滑，即Gtanθ≤2μG，解得：tanθ≤2μ，故C正确；若保持θ=45°不变，圆柱体的重力增大△G，则N′=（G+△G），底座C受到的静摩擦力刚好达到最大静摩擦力，保持底座C静止，根据平衡条件得： N′=μ（G+N′），解得：△Gm=G．故D正确；故选CD．