题目内容
摩天大楼中一部直通高层的客运电梯，行程超过百米，电梯的简化模型如图11甲所示。考虑安全、舒适、省时等因素，电梯的加速度a是随时间t变化的。已知电梯在t＝0时由静止开始上升，a－t图象如图11乙所示。电梯总质量m＝2.0×103 kg。忽略一切阻力，重力加速度g取10 m/s2。
(1)求电梯在上升过程中受到的最大拉力F1和最小拉力F2；
(2)类比是一种常用的研究方法。对于直线运动，教科书中讲解了由v－t图象求位移的方法。请你借鉴此方法，对比加速度和速度的定义，根据图乙所示a－t图象，求电梯在第1 s内的速度改变量Δv1和第2 s末的速率v2。
图11
解析：(1)由牛顿第二定律，有F－mg＝ma
由a－t图象可知，F1和F2对应的加速度分别是a1＝1.0 m/s2，a2＝－1.0 m/s2，
F1＝m(g＋a1)＝2.0×103×(10＋1.0)N＝2.2×104 N
F2＝m(g＋a2)＝2.0×103×(10－1.0)N＝1.8×104 N
(2)类比可得，所求速度变化量等于第1 s内a－t图线下的面积，Δv1＝0.5 m/s
同理可得Δv2＝v2－v0＝1.5 m/s
v0＝0，第2 s末的速率v2＝1.5 m/s
答案：(1)F1＝2.2×104 N F2＝1.8×104 N (2) Δv1＝0.5 m/s v2＝1.5 m/s
练习册系列答案
相关题目
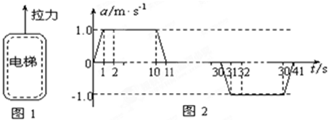摩天大楼中一部直通高层的客运电梯．行程超过百米．电梯的简化模型如下所示．电梯的加速度a随时间t变化的．已知电梯在t=0时由静止开始上升，a一t图象如图2所示．电梯总质最m=2.0x103kg．忽略一切阻力．重力加速度g取10m/s2．求
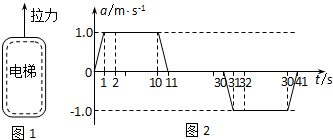摩天大楼中一部直通高层的客运电梯，行程超过百米．电梯的简化模型如图1所示．考虑安全、舒适、省时等因素，电梯的加速度a是随时间t变化的，已知电梯在t=0时由静止开始上升，a─t图象如图2所示．电梯总质量m=2.0×103kg．忽略一切阻力，重力加速度g取10m/s2．
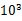kg。忽略一切阻力，重力加速度g取10m/s2。
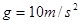，求：
；
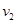