题目内容
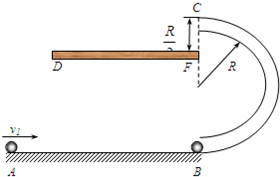 如图所示,一质量m1=0.2kg的小球,从光滑水平轨道上的一端A处,以v1=2.5m/s的速度水平向右运动.轨道的另一端B处固定放置一竖直光滑半圆环轨道(圆环半径比细管的内径大得多),轨道的半径R=10cm,圆环轨道的最低点与水平轨道相切;空中有一固定长为15cm的木板DF,F在轨道最高点C的正下方,竖直距离为5cm.水平轨道的另一端B处有一质量m2=0.2kg的小球,m1、m2两小球在B处发生的是完全弹性碰撞,重力加速度为g=10m/s2,求:
如图所示,一质量m1=0.2kg的小球,从光滑水平轨道上的一端A处,以v1=2.5m/s的速度水平向右运动.轨道的另一端B处固定放置一竖直光滑半圆环轨道(圆环半径比细管的内径大得多),轨道的半径R=10cm,圆环轨道的最低点与水平轨道相切;空中有一固定长为15cm的木板DF,F在轨道最高点C的正下方,竖直距离为5cm.水平轨道的另一端B处有一质量m2=0.2kg的小球,m1、m2两小球在B处发生的是完全弹性碰撞,重力加速度为g=10m/s2,求:(1)经过C点时,小球m2对轨道的作用力的大小及方向?
(2)m2小球打到木板DF上的位置?
分析:(1)在B处m1与m2发生的是完全弹性碰撞,根据动量守恒定律及能量守恒定律即可求解碰撞后B球的速度,由B到C的过程,根据机械能守恒,求出C点速度,再根据向心力公式即可求解;
(2)小球从C飞出做平抛运动,根据平抛运动的基本规律即可求解.
(2)小球从C飞出做平抛运动,根据平抛运动的基本规律即可求解.
解答: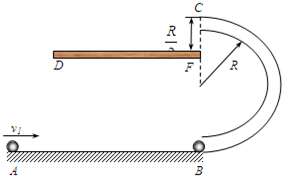 解:(1)在B处m1与m2发生的是完全弹性碰撞,有
解:(1)在B处m1与m2发生的是完全弹性碰撞,有
m1v1=m1v1′+m2v2′①
m1v12=
m1v1′2+
m2v2′2 ②
由①②式解得:
v1′=0,v2′=v1=2.5m/s
由B到C的过程,机械能守恒,有
m2v2′2=m2g2R+
m2vC2
带入数据得:vC=1.5m/s
在C点对m2,根据向心力公式得:
m2g+N=m2
带入数据解得:N=2.5N
据牛顿第三定律知:小球对轨道的作用力大小为2.5N,方向竖直向上;
(2)小球从C飞出做平抛运动,有
vC=
gt2=
带入数据解得:x=0.15m=15cm,所以物体刚好落在木板的D点上.
答:(1)经过C点时,小球m2对轨道的作用力大小为2.5N,方向竖直向上;
(2)m2小球打到木板DF上的D点.
 解:(1)在B处m1与m2发生的是完全弹性碰撞,有
解:(1)在B处m1与m2发生的是完全弹性碰撞,有m1v1=m1v1′+m2v2′①
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由①②式解得:
v1′=0,v2′=v1=2.5m/s
由B到C的过程,机械能守恒,有
| 1 |
| 2 |
| 1 |
| 2 |
带入数据得:vC=1.5m/s
在C点对m2,根据向心力公式得:
m2g+N=m2
| vC2 |
| R |
带入数据解得:N=2.5N
据牛顿第三定律知:小球对轨道的作用力大小为2.5N,方向竖直向上;
(2)小球从C飞出做平抛运动,有
vC=
| x |
| t |
| 1 |
| 2 |
| R |
| 2 |
带入数据解得:x=0.15m=15cm,所以物体刚好落在木板的D点上.
答:(1)经过C点时,小球m2对轨道的作用力大小为2.5N,方向竖直向上;
(2)m2小球打到木板DF上的D点.
点评:本题主要考查了动量守恒、平抛运动、机械能守恒定律、向心力公式及运动学基本公式的应用,综合性较强,难度适中.题中因m1与m2发生的是完全弹性碰撞,所以碰撞后两球交换速度.

练习册系列答案
相关题目
 (2013?烟台二模)如图所示,一质量m1=0.45kg的平板小车静止在光滑的水平轨道上.车上右端放一质量m2=0.2kg的小物体,小物体可视为质点.现有一质量m0=0.05kg的子弹以水平速度v0=100m/s射中小车左端,并留在车中,最终小物块以5m/s的速度与小车脱离.子弹与车相互作用时间很短,g取10m/s2.求:
(2013?烟台二模)如图所示,一质量m1=0.45kg的平板小车静止在光滑的水平轨道上.车上右端放一质量m2=0.2kg的小物体,小物体可视为质点.现有一质量m0=0.05kg的子弹以水平速度v0=100m/s射中小车左端,并留在车中,最终小物块以5m/s的速度与小车脱离.子弹与车相互作用时间很短,g取10m/s2.求: 如图所示,一质量m1=0.45kg的平顶小车静止在光滑的水平轨道上.车顶右端放一质量m2=0.2kg的小物块,小物体可视为质点.现有一质量m0=0.05kg的子弹以水平速度v0=100m/s射中小车左端,并留在车中,最终小车以8m/s的速度与小物块m2脱离.子弹与车相互作用时间很短.g取10m/s2.求:
如图所示,一质量m1=0.45kg的平顶小车静止在光滑的水平轨道上.车顶右端放一质量m2=0.2kg的小物块,小物体可视为质点.现有一质量m0=0.05kg的子弹以水平速度v0=100m/s射中小车左端,并留在车中,最终小车以8m/s的速度与小物块m2脱离.子弹与车相互作用时间很短.g取10m/s2.求: [物理-选修3-5]
[物理-选修3-5]