题目内容
【题目】如图所示,一半径为R的球体绕过球心O的轴O1O2以角速度ω匀速转动,A、B为球体上两点,OA与O1O2的夹角为60°,OB与O1O2的夹角为30°。则下列说法中正确的是
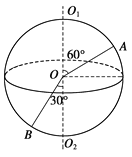
A. A、B两点具有相同的角速度
B. A、B两点具有相同的线速度
C. A、B两点具有相同的向心加速度
D. A、B两点的向心加速度方向都指向球心
【答案】A
【解析】A、A、B两点共轴转动,角速度相等,故A正确;
B、因为A、B两点绕地轴转动,A的转动半径大于B点的转动半径,根据![]() 知,A的线速度大于B的线速度大小,故B错误;
知,A的线速度大于B的线速度大小,故B错误;
C、根据![]() 知,角速度相等,A的转动半径大,则A点的向心加速度大于B点的向心加速度,故C错误;
知,角速度相等,A的转动半径大,则A点的向心加速度大于B点的向心加速度,故C错误;
D、A、B两点的向心加速度方向指向各自的圆心,即垂直指向地轴,故D错误。

练习册系列答案
相关题目