题目内容
17.如图是某绳波形成过程的示意图,1、2、3、4…为绳上的一系列等间距的质点,绳处于水平方向.质点1在外力作用下沿竖直方向做简谐运动,带动2、3、4…各个质点依次上下振动,把振动从绳的左端传到右端.t=0时质点1开始竖直向上运动,经过四分之一周期,质点5开始运动.下列判断正确的是( )
| A. | t=$\frac{T}{4}$时质点5的运动方向向下 | B. | t=$\frac{T}{2}$时质点8的加速度方向向下 | ||
| C. | t=$\frac{3T}{4}$时质点12的运动方向向下 | D. | t=T时质点17开始运动 |
分析 根据后一个质点重复前一个质点的振动,可知每一个质点开始振动的时候都和波源起振的情况相同;要求选项B,需知道该时刻该质点的位移的正负,再根据回复力F=-KX确定其加速度的方向;要知道t=$\frac{3}{4}$T质点的路程就必需知道该质点已运动多少时间即多少周期再根据一个周期内质点通过的路程为4A求解;要求t=T时质点9运动的方向需知道该时刻质点9已运动的时间从而确定其运动的方向.
解答 解:A、经过$\frac{T}{4}$时,质点1从平衡位置运动到波峰,由于后一个质点重复前一个质点的振动,由于质点1开始振动时是从平衡位置开始向上振动,故质点5开始振动时也是由平衡位置开始向上振动.故A错误.
B、振动从质点1传播到质点5经过$\frac{T}{4}$,质点1和质点5之间的距离为$\frac{1}{4}$λ,质点1到质点8的距离为$\frac{7}{16}$λ,所以波从质点1传到质点8所需时间为$\frac{7}{16}$T,开始时质点8向上振动,故在t=$\frac{T}{2}$时质点8已振动了$\frac{T}{2}$-$\frac{7}{16}$T=$\frac{1}{16}$T,即质点8在从平衡位置向波峰的运动过程中,根据a=-$\frac{kx}{m}$,得知加速度方向向下.故B正确.
C、质点1和质点12之间的距离为$\frac{11}{16}$λ,在 t=$\frac{3}{4}$T时刻,质点12已运动了 $\frac{3}{4}$T-$\frac{11}{16}$T=$\frac{1}{16}$T,开始时质点12向上振动,故在t=$\frac{3}{4}$T时刻,质点12的运动方向向上.故C错误.
D、一个周期内振动的距离等于一个波长,则知t=T时质点17开始振动,故D正确.
故选:BD.
点评 根据简谐波形成的碦:后一个质点重复前一个质点的振动”、“一个周期内质点通过的路程为4A”是解决此类问题的关键所在.

①运行的时间相等 ②加速度相同 ③落地时的速度相同 ④落地时的动能相等.
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
| A. | 位移的大小可能小于4m | B. | 位移的大小不可能大于10m | ||
| C. | 加速度的大小可能小于4m/s2 | D. | 加速度的大小可能大于10m/s2 |
| A. | 当振子再次与零时刻的速度相同时,经过的时间一定是一个周期 | |
| B. | 当振子再次经过P时,经过的时间一定是半周期 | |
| C. | 当振子的加速度再次与零时刻的加速度相同时,一定又到达位置P | |
| D. | 一定还有另一个位置跟位置P有相同的位移 |
 如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )
如图所示,甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )| A. | 该波的传播速率为4 m/s | |
| B. | 该波的传播方向沿x轴正方向 | |
| C. | 经过0.5 s时间,质点P沿波的传播方向向前传播2 m | |
| D. | 该波在传播过程中若遇到8 m的障碍物,能发生明显衍射现象 |
| A. | 离太阳越近的行星周期越大 | |
| B. | 离太阳越远的行星周期越小 | |
| C. | 离太阳越近的行星的向心加速度越大 | |
| D. | 以上说法都不对 |
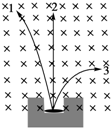 在贝克勒尔发现天然放射现象后,人们对三种放射线的性质进行了深入研究,如图为三种射线在同一磁场中的运动轨迹,判断射线名称:
在贝克勒尔发现天然放射现象后,人们对三种放射线的性质进行了深入研究,如图为三种射线在同一磁场中的运动轨迹,判断射线名称: