题目内容
18.物体作匀变速直线运动的初速度为v0,末速度为vt,试证明:该物体在某段时间t的中点时刻的瞬时速度等于这段时间内的平均速度,即:v${\;}_{\frac{t}{2}}$=$\overline{v}$=$\frac{{v}_{0}+{v}_{t}}{2}$.分析 根据位移时间公式的表达式,结合平均速度的定义式求出平均速度的大小,通过速度时间公式得出中间时刻的瞬时速度,判断是否相等.
解答 证明:设物体在上述两个T内的总位移为s,则$s={v_0}•2T+\frac{1}{2}a{(2T)^2}$
物体在这两个T内的平均速度为$\overline{v}=\frac{s}{2T}={v_0}+aT={v_T}$
而v0+aT=$\frac{{v}_{0}+{v}_{0}+2aT}{2}$=$\frac{{v}_{0}+{v}_{t}}{2}$
故可证vT即为2T时间内的中间时刻的瞬时速度即$\overrightarrow{v}$=vT=$\frac{{v}_{0}+{v}_{t}}{2}$.
点评 解决本题的关键知道匀变速直线运动的推论及推导过程,对于这些重要推论不能只局限于知道和会用,而应掌握其推导过程;以便于更好的应用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
8.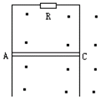 图中回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的说法有( )
图中回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的说法有( )
 图中回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的说法有( )
图中回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外,导体AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的说法有( )| A. | 导体下落过程中,机械能守恒 | |
| B. | 导体加速下落过程中,导体减少的重力势能全部转化为在电阻上产生的热量 | |
| C. | 导体加速下落过程中,导体减少的重力势能转化为导体增加的动能和回路中产生的热 | |
| D. | 导体达到稳定速度后的下落过程中,导体减少的重力势能全部转化为回路中产生的热 |
13. 如图所示,在μ=0.2的粗糙水平面上,有一质量为10kg的物体以一定的速度向左运动,同时还有一水平向右的力F作用于物体上,其大小为10N,则物体受到的摩擦力为(g取10m/s2)( )
如图所示,在μ=0.2的粗糙水平面上,有一质量为10kg的物体以一定的速度向左运动,同时还有一水平向右的力F作用于物体上,其大小为10N,则物体受到的摩擦力为(g取10m/s2)( )
 如图所示,在μ=0.2的粗糙水平面上,有一质量为10kg的物体以一定的速度向左运动,同时还有一水平向右的力F作用于物体上,其大小为10N,则物体受到的摩擦力为(g取10m/s2)( )
如图所示,在μ=0.2的粗糙水平面上,有一质量为10kg的物体以一定的速度向左运动,同时还有一水平向右的力F作用于物体上,其大小为10N,则物体受到的摩擦力为(g取10m/s2)( )| A. | 大小为10N,方向向右 | B. | 大小为10N,方向向左 | ||
| C. | 大小为20N,方向向右 | D. | 大小为20N,方向向左 |
3.如图所示为一简谐横波的波动图象,已知波速v=60m/s,且沿x轴正方向传播,由图可知 ( )

| A. | 各质点的振幅为2cm,波长是24m,周期是2.5s | |
| B. | 在x=6m处质点的位移为零,速度方向沿x轴正方向 | |
| C. | 在x=18m处质点的位移为零,速度最大 | |
| D. | 在x=24m处质点的位移为2cm,振动周期是0.4s |
10. 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g砝码时,指针指示的刻度数值记作L2;…;挂七个50g砝码时,指针指示的刻度数值记作L7.表记录的是该同学已测出的6个值.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g砝码时,指针指示的刻度数值记作L2;…;挂七个50g砝码时,指针指示的刻度数值记作L7.表记录的是该同学已测出的6个值.
测量记录表:
(1)实验中,L3和L7两个值还没有测定,请你根据如图所示将这两个测量值填入记录表中.
(2)为了充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值:d4=L7-L3=7.20cm.
(3)根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{{{d_1}+{d_2}+{d_3}+{d_4}}}{4×4}$.代入数据解得△L=1.75 cm.
(4)计算弹簧的劲度系数k=28N/m.(g取9.8N/kg)
 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g砝码时,指针指示的刻度数值记作L2;…;挂七个50g砝码时,指针指示的刻度数值记作L7.表记录的是该同学已测出的6个值.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g砝码时,指针指示的刻度数值记作L2;…;挂七个50g砝码时,指针指示的刻度数值记作L7.表记录的是该同学已测出的6个值.测量记录表:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.30 | 12.10 |
(2)为了充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm.请你给出第四个差值:d4=L7-L3=7.20cm.
(3)根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{{{d_1}+{d_2}+{d_3}+{d_4}}}{4×4}$.代入数据解得△L=1.75 cm.
(4)计算弹簧的劲度系数k=28N/m.(g取9.8N/kg)
7.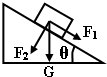 重力为G的物体静止在倾角为θ的斜面上,将重力G分解为垂直斜面向下的力F2和沿斜面向下的力F1,那么( )
重力为G的物体静止在倾角为θ的斜面上,将重力G分解为垂直斜面向下的力F2和沿斜面向下的力F1,那么( )
 重力为G的物体静止在倾角为θ的斜面上,将重力G分解为垂直斜面向下的力F2和沿斜面向下的力F1,那么( )
重力为G的物体静止在倾角为θ的斜面上,将重力G分解为垂直斜面向下的力F2和沿斜面向下的力F1,那么( )| A. | 物体对斜面的压力方向与F2方向相同 | |
| B. | F2就是物体对斜面的压力 | |
| C. | 重力沿斜面向下的分力F1与斜面对物体的静摩擦力是一对平衡力 | |
| D. | 物体受到重力、斜面对物体的支持力、静摩擦力、F1和F2共五个力的作用 |
8.下列物理量是矢量的是( )
| A. | 功 | B. | 功率 | C. | 动能 | D. | 加速度 |
 在测物体的加速度试验中,小车拖着纸带运动,打点计时器每隔0.02s打一个点,打出的纸带如图所示.选出A,B,C,D,E共5个计数点,每相邻两个计数点之间还有四个实验点图中未画出,以A点为起点量出的到各点的位移已标在图上.由此可求得小车运动的加速度a=0.20m/s2,打下A点时小车运动的速度为vA=0.15m/s.
在测物体的加速度试验中,小车拖着纸带运动,打点计时器每隔0.02s打一个点,打出的纸带如图所示.选出A,B,C,D,E共5个计数点,每相邻两个计数点之间还有四个实验点图中未画出,以A点为起点量出的到各点的位移已标在图上.由此可求得小车运动的加速度a=0.20m/s2,打下A点时小车运动的速度为vA=0.15m/s. 如图所示,a为内接法(“内接法、外接法”),测量大电阻(“大、小”),R测大于R真 (“>、=、<”)
如图所示,a为内接法(“内接法、外接法”),测量大电阻(“大、小”),R测大于R真 (“>、=、<”)