题目内容
I.有同学利用如图所示的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的质量相等,当系统达到平衡-时,根据钩码个数读出三根绳子的拉力TOA、TOB和TOC,回答下列问题:(1)改变钩码个数,实验能完成的是______
A.钩码的个数N1=N2=2,N3=4
B.钩码的个数N1=N3=3,N2=4
C.钩码的个数N1=N2=N3=4
D.钩码的个数N1=3,N2=4,N3=5
(2)在拆下钩码和绳子前,应该做好三个方面的记录:
______;
______;
______.
II.有两组同学进行了如下实验:
(1)甲组同学器材有:电源,滑动变阻器,电流表A1(0-200mA,内阻约11Ω),电流表A2(0-300mA,内阻约8Ω,定值电阻R1=24Ω,R2=12Ω,开关一个,导线若干.为了测量A1的内阻,该组同学共设计了下图中A、B、C、D四套方案:

其中最佳的方案是______套,若用此方案测得A1、A2示数分别为180mA和270mA,则A1的内阻为______Ω.
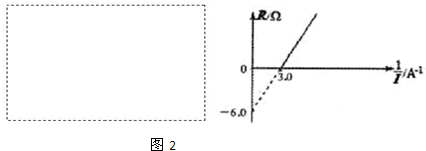
(2)乙组同学将甲组同学的电流表A1拿过来,再加上电阻箱R(最大阻值9.9Ω),定值电阻R=6.0Ω,一个开关和若干导线用来测量一个电源(电动势E约为6.2V,内阻r约为2.1Ω)的电动势及内阻.请在图2方框中画出设计电路图.
若记录实验中电阻箱的阻值R和对应的A1示数的倒数
 ,得到多组数据后描点作出R-
,得到多组数据后描点作出R- 图线如图2所示,则该电源的电动势E=______V,内阻r=______Ω.(结果保留两位有效数字)
图线如图2所示,则该电源的电动势E=______V,内阻r=______Ω.(结果保留两位有效数字)

【答案】分析:I、分析题意,由题意明确实验的原理,再根据力的合成与分解的知识分析实验中的数据及注意事项;
II、(1)由题意明确实验原理,根据实验仪器及实验中给出的电路图可选出最优的电路;
(2)要想测出电源的电动势和内电阻,只需找出电源两端的电压及流过电流的电流即可,根据题目中给出的条件可以采用安阻法进行测量; 由闭合电路欧姆律可得出表达式,根据数形关系可求得电动势和内电阻.
解答: 解:I、(1)由题意可知,本实验通过钩码的重力充当拉力,而N3为合力,N1与N2为分力,则根据共点力的合成知识可知,二分力的代数和应大于合力,两分力的差应小于第三力,故符合条件的只有BCD;
解:I、(1)由题意可知,本实验通过钩码的重力充当拉力,而N3为合力,N1与N2为分力,则根据共点力的合成知识可知,二分力的代数和应大于合力,两分力的差应小于第三力,故符合条件的只有BCD;
(2)在探究合力与分力的关系时,需要明确三个力的大小及方向,故在实验中需记录下结点O的位置;两绳子的方向及钩码的重力;
II.(1)要想测得A1的内阻应测出流过其中的电流及两端的电压,但由题意可知,题目中没有给出电压表,故可以考虑采用两个电流表充当电压表进行测量;图中AB采用了此种方法,但是由于两电流表内阻均不是已知量,只是约数,无法正确测出电阻值;
故可以采用并联电路的分流原理,则定值电阻分流,则可通过并联电路的电流规律求得并联部分的电压;CD采用的即为此种方法;C中分流电阻采用了12Ω的电阻,则电流表A2中流过的电流为A1中电流的两倍;容易损坏电表;而D中采用了大电阻,则A1满偏时,A2中电流约为: ×200mA=290mA;则能准确的得出数据,故选D方案为最佳方案;
×200mA=290mA;则能准确的得出数据,故选D方案为最佳方案;
由并联电路的规律可知,定值电阻中的电流为270-180=90mA;则电流表内阻RA=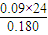 =12Ω;
=12Ω;
(2)测电动势和内电阻需要得出路端电压和电流;但若把电阻箱和电源串联,电路中最小电流为 =250mA,超过A1的量程,故应采用定值电阻分流;电路如图所示;
=250mA,超过A1的量程,故应采用定值电阻分流;电路如图所示;
故闭合电路欧姆定律可知:I=
 ,则变形得:
,则变形得:
R= -4-r;故图象中的斜率等于
-4-r;故图象中的斜率等于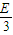 =2.0;故E=6.0V;
=2.0;故E=6.0V;
图象与纵坐标的交点为-6.0=-r-4
解得r=2;
故答案为:I、(1)BCD;(2)标记结点O的位置;纪录OA、OB、OC三段绳子的方向;记录三段绳子所挂钩码的个数;II、(1)D,12;(2)6.0;2.0.
点评:本题为探究型实验,要求学生有较高的审题能力、归纳能力;注意在解题时应灵活应用我们所学过的规律,并能迁移使用,本题的难度较大.
II、(1)由题意明确实验原理,根据实验仪器及实验中给出的电路图可选出最优的电路;
(2)要想测出电源的电动势和内电阻,只需找出电源两端的电压及流过电流的电流即可,根据题目中给出的条件可以采用安阻法进行测量; 由闭合电路欧姆律可得出表达式,根据数形关系可求得电动势和内电阻.
解答:
 解:I、(1)由题意可知,本实验通过钩码的重力充当拉力,而N3为合力,N1与N2为分力,则根据共点力的合成知识可知,二分力的代数和应大于合力,两分力的差应小于第三力,故符合条件的只有BCD;
解:I、(1)由题意可知,本实验通过钩码的重力充当拉力,而N3为合力,N1与N2为分力,则根据共点力的合成知识可知,二分力的代数和应大于合力,两分力的差应小于第三力,故符合条件的只有BCD; (2)在探究合力与分力的关系时,需要明确三个力的大小及方向,故在实验中需记录下结点O的位置;两绳子的方向及钩码的重力;
II.(1)要想测得A1的内阻应测出流过其中的电流及两端的电压,但由题意可知,题目中没有给出电压表,故可以考虑采用两个电流表充当电压表进行测量;图中AB采用了此种方法,但是由于两电流表内阻均不是已知量,只是约数,无法正确测出电阻值;
故可以采用并联电路的分流原理,则定值电阻分流,则可通过并联电路的电流规律求得并联部分的电压;CD采用的即为此种方法;C中分流电阻采用了12Ω的电阻,则电流表A2中流过的电流为A1中电流的两倍;容易损坏电表;而D中采用了大电阻,则A1满偏时,A2中电流约为:
 ×200mA=290mA;则能准确的得出数据,故选D方案为最佳方案;
×200mA=290mA;则能准确的得出数据,故选D方案为最佳方案;由并联电路的规律可知,定值电阻中的电流为270-180=90mA;则电流表内阻RA=
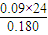 =12Ω;
=12Ω;(2)测电动势和内电阻需要得出路端电压和电流;但若把电阻箱和电源串联,电路中最小电流为
 =250mA,超过A1的量程,故应采用定值电阻分流;电路如图所示;
=250mA,超过A1的量程,故应采用定值电阻分流;电路如图所示;故闭合电路欧姆定律可知:I=

 ,则变形得:
,则变形得:R=
 -4-r;故图象中的斜率等于
-4-r;故图象中的斜率等于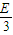 =2.0;故E=6.0V;
=2.0;故E=6.0V;图象与纵坐标的交点为-6.0=-r-4
解得r=2;
故答案为:I、(1)BCD;(2)标记结点O的位置;纪录OA、OB、OC三段绳子的方向;记录三段绳子所挂钩码的个数;II、(1)D,12;(2)6.0;2.0.
点评:本题为探究型实验,要求学生有较高的审题能力、归纳能力;注意在解题时应灵活应用我们所学过的规律,并能迁移使用,本题的难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某同学利用如图所示的电路,研究加在标有“3.8 V0.3 A ”的小电珠两端的电压和通过它的电流的关系,得到如下表所示的数据.

| 1 | 2 | 3 | 4 | 5 | 6 |
U/V | 0 | 0.100 | 0.200 | 0.40 | 0.60 | 1.00 |
I/A | 0 | 0.050 | 0.100 | 0.124 | 0.140 | 0.160 |
| 7 | 8 | 9 | 10 | 11 | 12 |
U/V | 1.60 | 2.20 | 2.60 | 3.00 | 3.40 | 3.80 |
I/A | 0.200 | 0.230 | 0.258 | 0.274 | 0.290 | 0.310 |
由这些数据可以得到:
(1)描绘出小电珠的I-U曲线.
(2)比较U1=1.0 V和U2=3.0 V的小电珠的电阻的大小,并说明其原因.
(3)小电珠两端的电压从零到额定电压变化时,小电珠的最大电阻是多少?最大电功率是多少?
(4)通过小电珠的电流等于零时,这个小电珠的电阻是多少?
 I.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.
I.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.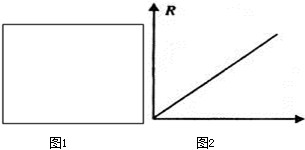
 I.有同学利用如图所示的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的质量相等,当系统达到平衡-时,根据钩码个数读出三根绳子的拉力TOA、TOB和TOC,回答下列问题:
I.有同学利用如图所示的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的质量相等,当系统达到平衡-时,根据钩码个数读出三根绳子的拉力TOA、TOB和TOC,回答下列问题: