题目内容
7.在“测定金属的电阻率”实验中,需要测金属丝的长度L,直径d和电阻Rx.
①请写出测金属丝电阻率的表达式P=$\frac{π{R}_{x}{d}^{2}}{4L}$(用上述测量量字母表示);
②测量金属丝长度时,刻度尺示数如图甲所示,则测量值L=46.60cm;
③测量金属丝直径时,螺旋测微器如图乙所示,调节部件C,使测微螺杆接触金属丝,接下来应调节部件D,再拨动部件B,最后读数.测量结果如图丙所示,则测量值d=0.905mm.
④用伏安法测金属丝的电阻时,由于电压表、电流表内阻的影响,不论使用内接法还是外接法,都会产生系统误差.按如图丁所示的电路进行测量,可以消除由于电表内阻造成的系统误差.利用该电路进行实验的主要操作过程是:
第一步:先将滑动变阻器R的滑动头调到最左端,单刀双掷开关S2接“1”,闭合开关S,调节R,使电压表和电流表的示数尽量大些,读出此时电压表和电流表的示数U1,I1;
第二步:将S2切换到“2”,读出此时电压表和电流表的示数U2,I2;
则金属丝电阻的计算式Rx=_$\frac{{U}_{1}}{{I}_{1}}-\frac{{U}_{2}}{{I}_{2}}$(用上述电表的示数表示).
分析 ①根据电阻定律求出电阻率的表达式;
②根据图示刻度尺确定其分度值,金属丝两端点所对应刻度尺示数之差是金属丝的长度;
③适用螺旋测微器时,选旋动粗调旋钮,再转到微调旋钮,最后拨动止动旋钮固定后读数.螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数.
④单刀双掷开关S2合向1,由电压表和电流表的示数U1和I1,可求出Rx、电流表、变阻器串联的电阻.
将单刀双掷开关S2合向2,读出此时电压表和电流表的示数U2和I2,可求出电流表和变阻器串联的电阻.
两个阻值之差等于被测电阻.根据欧姆定律写出表达式.
解答 解:①由电阻定律可知,金属丝电阻Rx=ρ$\frac{L}{S}$=ρ$\frac{L}{π(\frac{d}{2})^{2}}$,则金属丝电阻率ρ=$\frac{π{R}_{x}{d}^{2}}{4L}$;
②由图示刻度尺可知,其分度值为1mm,金属丝的长度L=46.60cm;
③用螺旋测微器测电阻丝的直径时,先转动粗调旋钮C使测微螺杆接近被测电阻丝,再转到微调旋钮D夹住被测物,直到棘轮发出声音为止,拨动止动旋钮B使螺杆固定后读数.
由图示螺旋测微器可知,螺旋测微器固定刻度示数为0.5mm,可动刻度示数为40.5×0.01mm=0.405mm,螺旋测微器示数为0.5mm+0.405m=0.905mm;
④将单刀双掷开关S2合向1时,电压表和电流表的示数U1、I1.根据欧姆定律得:
Rx+RA+R1=$\frac{{U}_{1}}{{I}_{1}}$;
将单刀双掷开关S2向2闭合时,电压表和电流表的示数U2、I2.根据欧姆定律得:
RA+R1=$\frac{{U}_{2}}{{I}_{2}}$
联立上两式得:Rx=$\frac{{U}_{1}}{{I}_{1}}-\frac{{U}_{2}}{{I}_{2}}$.
故答案为:①$\frac{π{R}_{x}{d}^{2}}{4L}$; ②46.60;③D;B;0.905;④$\frac{{U}_{1}}{{I}_{1}}-\frac{{U}_{2}}{{I}_{2}}$.
点评 本题考查了电阻定律的应用、刻度尺与螺旋测微器的读数,应用电阻定律即可求出电阻率的表达式;螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数,螺旋测微器需要估读.

| A. | 乙的质量等于甲的质量时,碰撞后乙的速率为v1 | |
| B. | 乙的质量远远小于甲的质量时,碰撞后乙的速率为2v1 | |
| C. | 乙的质量远远小于甲的质量时,碰撞后乙的速率为v1 | |
| D. | 碰撞过程中甲对乙做功大于乙动能的增量 |
| A. | 小于临界体积的铀块不可能发生链式反应 | |
| B. | 在核反应方程${\;}_{0}^{1}$n+${\;}_{3}^{6}$Li→${\;}_{1}^{3}$H+X中,X为α粒子 | |
| C. | 阴极射线是原子核内的中子转变为质子时产生的高速电子流 | |
| D. | 用频率大于某金属极限频率的单色光照射该金属,若增大入射光的频率,则逸出的光电子数目一定增多 | |
| E. | 按照波尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,原子的总能量增大 |
 光滑水平面上有一边长为L的正方形区域处在电场强度为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平速度V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能不可能为( )
光滑水平面上有一边长为L的正方形区域处在电场强度为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平速度V0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能不可能为( )| A. | $\frac{1}{2}$mv02 | B. | $\frac{1}{2}$mv02-qEL | C. | $\frac{1}{2}$mv02+$\frac{2}{3}$qEL | D. | $\frac{1}{2}$mv02+$\frac{1}{4}$qEL |
| A. | 振幅一定为A | |
| B. | 周期一定为T | |
| C. | 速度的最大值一定为v | |
| D. | 开始振动的方向沿y轴向上或向下取决于它离波源的距离 | |
| E. | 若p点与波源距离s=vT,则质点p的振动位移总与波源的振动位移相同 |


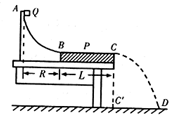 测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的较光滑四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度大小为g.实验步骤如下:
测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的较光滑四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度大小为g.实验步骤如下: