题目内容
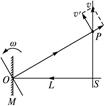
如图所示,平面镜M与竖直巨型光屏平行放置,其与光屏之间的距离为L,由小孔S处垂直光屏向平面镜中点O射入一束氦氖激光,现平面镜M以其中点O为轴逆时针匀速旋转,角速度为ω,求：
(1)平面镜转过15°时,光屏上形成的光点P至S的距离.
(2)平面镜转动时间t(t<
)时,激光束在光屏上形成的光点移动的速度.
(1)平面镜转过15°时,光屏上形成的光点P至S的距离.
(2)平面镜转动时间t(t<
)时,激光束在光屏上形成的光点移动的速度.(1)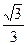
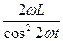
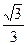L (2)
L (2)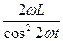(1)平面镜转过15°角,则反射光线转过30°角,由几何关系可知：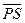
=L·tan30°=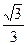L.
(2)平面镜转动时间t,则反射光线转过的角度为：θ=2ω·t
光点P离O点的距离
sOP=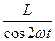
光点P绕点O旋转的线速度
v=2ω·sOP=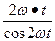
由速度的合成与分解的知识可知,P点在光屏上移动的速度v满足：
v=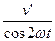
=
.
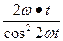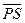=L·tan30°=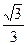L.(2)平面镜转动时间t,则反射光线转过的角度为：θ=2ω·t
光点P离O点的距离
sOP=
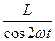
光点P绕点O旋转的线速度
v=2ω·sOP=
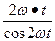
由速度的合成与分解的知识可知,P点在光屏上移动的速度v满足：
v=
=. 
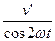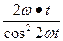练习册系列答案
相关题目
的平行细光束以相同的入射角射到成
角的平行玻璃砖上表面，则从玻璃砖下表面射出的光线：
a
a
a
