题目内容
(15分)如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏离竖直方向的最大角度θ=74°。
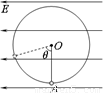
⑴求电场强度的大小E;
⑵求小球向左摆动的过程中,对细线拉力的最大值;
⑶若从A点处释放小球时,给小球一个水平向左的初速度v0,则为保证小球在运动过程中,细线不会松弛,v0的大小应满足什么条件?
⑴E=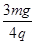 ;⑵T ′=
;⑵T ′=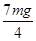 ;⑶v0≤
;⑶v0≤ 或v0≥
或v0≥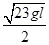
【解析】
试题分析:⑴设小球最大摆角位置为C,在整个过程中,小球受重力mg、电场力qE和细线的拉力T作用,拉力T始终不做功,在小球由A运动至C的过程中,根据动能定理有:qElsinθ-mgl(1-cosθ)=0-0
解得:E=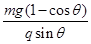 =
=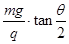 =
=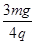
⑵重力与电场力的合力大小为:F=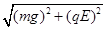 =
=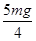 ①
①
其方向指向左下方,设与竖直方向成α角,根据几何关系有:tanα=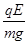 =
=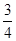 ,即α=37°
②
,即α=37°
②
当小球摆动至细线沿此方向,设为B位置时,小球对细线的拉力最大,则:T-F=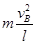 ③
③
小球在由A运动至B的过程中,根据动能定理有:Fl(1-cosα)=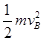 -0 ④
-0 ④
根据牛顿第三定律可知,小球对细线的拉力为:T ′=T ⑤
由①②③④⑤式联立解得:T ′=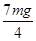
⑶要使细线不松弛有两种情况,当小球摆动过程中,细线的方向与F的方向不超过90°时,根据动能定理有:-Flcosα≤0-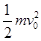
解得:v0≤ ⑥
⑥
当小球能完成完整的圆周运动时,需满足:F≤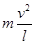 ⑦
⑦
根据动能定理有:-Fl(1+cosα)=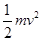 -
-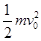 ⑧
⑧
由⑦⑧式联立解得:v0≥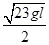 ⑨
⑨
由⑥⑨式联立解得,为保证小球在运动过程中,细线不松弛,v0的大小应满足的条件为:v0≤ 或v0≥
或v0≥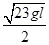
考点:本题主要考查了带电体在复合场中的运动问题,涉及动能定理、圆周运动向心力、牛顿运动定律的应用和临界条件的判断等知识,属于中档偏高题。


 。求:
。求:

 。求:
。求:
