题目内容
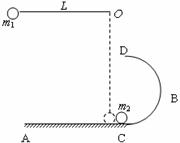
 如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.80m的细绳,一端固定于O点,另一端系一个质量m1为0.2 0kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.80kg的小铁球正碰,碰后m1小球以2.0m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求:
如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.80m的细绳,一端固定于O点,另一端系一个质量m1为0.2 0kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.80kg的小铁球正碰,碰后m1小球以2.0m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求:(1)m1刚摆到最低点时的速度
(2)m2在圆形轨道最低点C的速度为多大?
(3)光滑圆形轨道半径R应为多大?
分析:(1)球m1摆至最低点的过程中,根据机械能守恒定律求出到最低点时的速度.
(2)两个小球碰撞过程,根据动量守恒列式求碰后m2的速度.
(2)m2沿半圆形轨道运动,根据机械能守恒定律列式度.恰好能通过最高点D时,由重力提供向心力,由牛顿第二定律再次列式;最后联立求解可求出R.
(2)两个小球碰撞过程,根据动量守恒列式求碰后m2的速度.
(2)m2沿半圆形轨道运动,根据机械能守恒定律列式度.恰好能通过最高点D时,由重力提供向心力,由牛顿第二定律再次列式;最后联立求解可求出R.
解答:解:(1)设球m1摆至最低点时速度为v0,由小球机械能守恒,有:
m1gL=
m1
得:v0=
=
=4m/s
(2)m1与m2碰撞,动量守恒,设m1、m2碰后的速度分别为v1、v2.
选向右的方向为正方向,则:
m1v0=m1v1+m2v2
代入数值,有:0.2×4=0.2×(-2)+0.8×v2
解得:v2=1.5 m/s
(3)m2在CD轨道上运动时,由机械能守恒有:
m2
=m2g(2R)+
m2
①
由小球恰好通过最高点D点可知,重力提供向心力,即
m2g=m2
②
由①②解得:R=
=
=0.045m
答:
(1)m1刚摆到最低点时的速度为4m/s.
(2)m2在圆形轨道最低点C的速度为1.5m.
(3)光滑圆形轨道半径R应为0.045m.
m1gL=
| 1 |
| 2 |
| v | 2 0 |
得:v0=
| 2gL |
| 2×10×0.8 |
(2)m1与m2碰撞,动量守恒,设m1、m2碰后的速度分别为v1、v2.
选向右的方向为正方向,则:
m1v0=m1v1+m2v2
代入数值,有:0.2×4=0.2×(-2)+0.8×v2
解得:v2=1.5 m/s
(3)m2在CD轨道上运动时,由机械能守恒有:
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 D |
由小球恰好通过最高点D点可知,重力提供向心力,即
m2g=m2
| ||
| R |
由①②解得:R=
| ||
| 5g |
| 1.52 |
| 5×10 |
答:
(1)m1刚摆到最低点时的速度为4m/s.
(2)m2在圆形轨道最低点C的速度为1.5m.
(3)光滑圆形轨道半径R应为0.045m.
点评:本题主要考查了动量守恒、机械能守恒定律、向心力公式的应用,要知道小球恰好通过最高点时,由重力提供向心力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2008?珠海模拟)如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.8m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小铁球正碰,碰后m1小球以2m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求:
(2008?珠海模拟)如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.8m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小铁球正碰,碰后m1小球以2m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求:
 如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.8m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小铁球正碰,碰后m1小球以2m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求:
如图,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.8m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小铁球正碰,碰后m1小球以2m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10m/s2,求: