题目内容
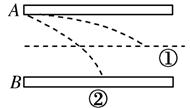
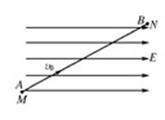
如右图所示，有一水平向右的匀强电场，场强为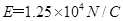
，一根长
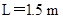、与水平方向的夹角为
的光滑绝缘细直杆MN固定在电场中，杆的下端M固定一个带电小球A，电荷量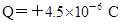
；另一带电小球B穿在杆上可自由滑动，电荷量
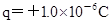，质量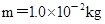
.现将小球B从杆的上端N静止释放，小球B开始运动．(静电力常量
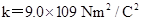，取
，
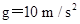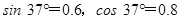)求：
(1)小球B开始运动时的加速度为多大？
(2)小球B的速度最大时，与M端的距离r为多大？
【答案】
(1) 
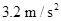(2)0.9 m
【解析】
试题分析：(1)开始运动时小球B受重力、库仑力、杆的弹力和电场力，沿杆方向运动，由牛顿第二定律得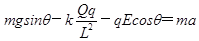
解得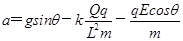
代入数据解得
.
(2)小球B速度最大时合力为零，即
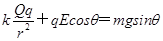
解得
代入数据解得
考点：带电粒子在电场中的运动，
点评：带电粒子在电场中的运动，综合了静电场和力学的知识，分析方法和力学的分析方法基本相同．先分析受力情况再分析运动状态和运动过程（平衡、加速、减速，直 线或曲线），然后选用恰当的规律解题．解决这类问题的基本方法有两种，第一种利用力和运动的观点，选用牛顿第二定律和运动学公式求解；第二种利用能量转化 的观点，选用动能定理和功能关系求解．
练习册系列答案
相关题目
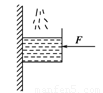
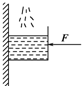如右图所示，有一重力不计的方形容器，被水平力F压在竖直的墙面上处于静止状态，现缓慢地向容器内注水，直到将容器刚好盛满为止，在此过程中容器始终保持静止，则下列说法中正确的是（ ）
