题目内容
如图所示,小球沿斜面向上运动,依次经过a、b、c、d后到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d 所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )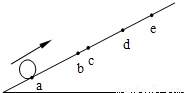
A.a=1m/s2
B.vc=3m/s
C.vb=2m/s
D.从d到e所用时间为4s
【答案】分析:本题的突破口是ab=bd=6m,bc=1m,小球从a到c的时间是2s,从a到d的时间是4s,根据x=vt+ at2即可求出va和a;再根据速度公式vt=v+at求出vc和vd,然后根据vt2-v2=2ax求出de的距离,最后根据vt=v+at求出从d到e的时间.
at2即可求出va和a;再根据速度公式vt=v+at求出vc和vd,然后根据vt2-v2=2ax求出de的距离,最后根据vt=v+at求出从d到e的时间.
解答:解:物体在a点时的速度大小为v,加速度为a,
则从a到c有xac=vt1+ at12
at12
即7=v×2+ ×a×4
×a×4
7=2v+2a
物体从a到d有xad=vt2+ at22
at22
即12=v×4+ a×16
a×16
3=v+2a
故a=- m/s2
m/s2
所以A错误;
故v=4m/s
根据速度公式vt=v+at可得
vc=4- ×2=3m/s
×2=3m/s
故B正确.
从a到b有
vb2-va2=2axab
解得vb=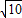 m/s
m/s
故C错误.
根据速度公式vt=v+at可得
vd=v+at2=4- ×4=2m/s
×4=2m/s
则从d到e有
-vd2=2axde
则xde=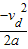 =4m
=4m
vt=v+at可得
从d到e的时间
tde=- =4s
=4s
故D正确.
故选:B、D.
点评:本题对运动学公式要求较高,要求学生对所有的运动学公式不仅要熟悉而且要熟练,要灵活,基本方法就是平时多练并且尽可能尝试一题多解.
 at2即可求出va和a;再根据速度公式vt=v+at求出vc和vd,然后根据vt2-v2=2ax求出de的距离,最后根据vt=v+at求出从d到e的时间.
at2即可求出va和a;再根据速度公式vt=v+at求出vc和vd,然后根据vt2-v2=2ax求出de的距离,最后根据vt=v+at求出从d到e的时间.解答:解:物体在a点时的速度大小为v,加速度为a,
则从a到c有xac=vt1+
 at12
at12即7=v×2+
 ×a×4
×a×47=2v+2a
物体从a到d有xad=vt2+
 at22
at22即12=v×4+
 a×16
a×163=v+2a
故a=-
 m/s2
m/s2所以A错误;
故v=4m/s
根据速度公式vt=v+at可得
vc=4-
 ×2=3m/s
×2=3m/s故B正确.
从a到b有
vb2-va2=2axab
解得vb=
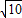 m/s
m/s故C错误.
根据速度公式vt=v+at可得
vd=v+at2=4-
 ×4=2m/s
×4=2m/s则从d到e有
-vd2=2axde
则xde=
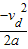 =4m
=4mvt=v+at可得
从d到e的时间
tde=-
 =4s
=4s故D正确.
故选:B、D.
点评:本题对运动学公式要求较高,要求学生对所有的运动学公式不仅要熟悉而且要熟练,要灵活,基本方法就是平时多练并且尽可能尝试一题多解.

练习册系列答案
相关题目
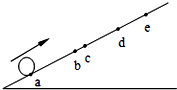 如图所示,小球沿斜面向上运动,依次经a、b、c、d到达最高点e.已知ab=bd=8m,bc=2m,小球从a到c和从c到d 所用的时间都是2s,则( )
如图所示,小球沿斜面向上运动,依次经a、b、c、d到达最高点e.已知ab=bd=8m,bc=2m,小球从a到c和从c到d 所用的时间都是2s,则( )| A、a=1m/s2 | B、vc=4m/s | C、de=2m | D、从d到e所用时间为3s |
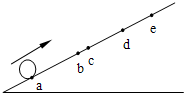 如图所示,小球沿斜面向上运动,依次经过a、b、c、d 到达最高点e,已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s.设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿斜面向上运动,依次经过a、b、c、d 到达最高点e,已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s.设小球经b、c时的速度分别为vb、vc,则( ) 如图所示,小球沿斜面向上运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d 所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则下列哪个选项正确的是( )
如图所示,小球沿斜面向上运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d 所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则下列哪个选项正确的是( )