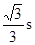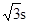题目内容
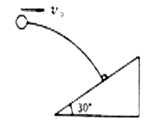
如图,轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上
的目标A。已知A点高度为h,山坡倾角为θ,重力加速度为g,由此可算出( )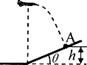
A.轰炸机的飞行高度 B.轰炸机的飞行速度
C.炸弹的飞行时间 D.炸弹投出时的动能
ABC
解析试题分析:由图可得炸弹的水平位移为 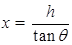 ;设轰炸机的飞行高度为H,炸弹的飞行时间为t,初速度为v0.据题:炸弹垂直击中山坡上的目标A,则根据速度的分解有:
;设轰炸机的飞行高度为H,炸弹的飞行时间为t,初速度为v0.据题:炸弹垂直击中山坡上的目标A,则根据速度的分解有: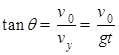
又  ;联立以上三式得:
;联立以上三式得: ,可知可以求出轰炸机的飞行高度H.
,可知可以求出轰炸机的飞行高度H.
炸弹的飞行时间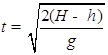 ,也可以求出t.轰炸机的飞行速度等于炸弹平抛运动的初速度,为
,也可以求出t.轰炸机的飞行速度等于炸弹平抛运动的初速度,为 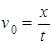 ,可知也可以求出.故A、B、C正确;由于炸弹的质量未知,则无法求出炸弹投出时的动能.故D错误。
,可知也可以求出.故A、B、C正确;由于炸弹的质量未知,则无法求出炸弹投出时的动能.故D错误。
考点:平抛运动的规律。

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案民族运动会上有一个骑射项目,运动员骑在奔驶的马背上,弯弓放箭射击侧向的固定目标M。假设运动员由A点沿AB方向骑马奔驰的速度为v1,运动员静止时射出的弓箭速度为v2,直线跑道离固定目标M的最近距离为d,要想在最短的时间内射中目标(不计空气阻力和重力影响),则运动员放箭处和射箭方向应该为( )
| A.在B处射出,箭头指向M |
| B.在B处射出,箭头指偏向A点的方向 |
| C.在AB间某处射出,箭头指向M |
| D.在AB间某处射出,箭头指向垂直于AB方向 |
如图,汽车以恒定的速度v0沿水平方向向右运动,车的末端通过绳拉物体A,当拉绳与水平方向的夹角为θ时,物体A上升速度v的大小为( )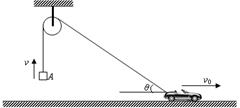
| A.v0/cosθ | B.v0/sinθ | C.v0cosθ | D.v0sinθ |
如图,x轴水平,y轴竖直。图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,若a、b、c的飞行时间分别为ta、tb、tc,抛出的初速度分别为va、vb、vc,则: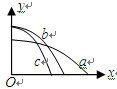
| A.ta>tb>tc | B.ta<tb=tc | C.va>vb=vc | D.va>vb>vc |
小球从地面上方某处水平抛出,抛出时的动能是7J,落地时的动能是28J,不计空气阻力,则小球落地时速度方向和水平方向的夹角是
| A.30° | B.37° | C.45° | D.60° |
在2014年索契冬奥会中国代表团收获3金4银2铜。在自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞离斜坡,在空中划过一段抛物线后,再落到雪坡上,如图所示。若雪坡的倾角为θ,飞出时的速度大小为v0,则以下说法错误的是
A.运动员在空中经历的时间是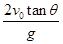 |
B.运动员的落点与起飞点的距离是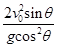 |
C.运动员的落点与起飞点间竖直高度是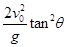 |
D.运动员落回雪坡时的速度大小是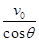 |
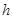 的平台上水平踢出一球,欲击中地面上A点。若两次踢球的方向均正确,第一次初速度为
的平台上水平踢出一球,欲击中地面上A点。若两次踢球的方向均正确,第一次初速度为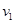 ,球的落点比
,球的落点比 近了
近了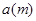 ;第二次球的落地点比
;第二次球的落地点比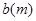 ,如图,试求:
,如图,试求: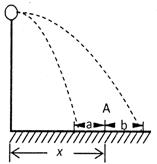
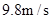 的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在
的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在 为
为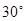 的斜面上,可知物体完成这段飞行的时间是( )
的斜面上,可知物体完成这段飞行的时间是( )