题目内容
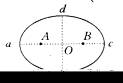
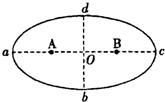
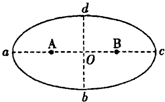
某行星绕太阳运动轨迹如图所示,图中A、B为椭圆轨迹的两个焦点,太阳位于A处,a为近日点,c为远日点,O为椭圆的几何中心,则行星( )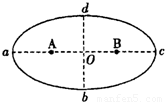
A.在a处的速率比在c处小
B.在a处的速率比在c处大
C.在a处的向心力等于万有引力
D.在b处的加速度方向指向O
【答案】分析:开普勒第二定律的内容,对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积. 如图所示,行星沿着椭圆轨道运行,太阳位于椭圆的一个焦点上.如果时间间隔相等,即t2-t1=t4-t3,那么面积A=面积B由此可知行星在远日点B的速率最小,在近日点A的速率最大.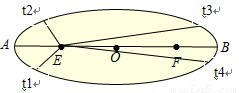
解答:解:A、B:根据开普勒第二定律,也称面积定律:在相等时间内,太阳和运动着的行星的连线所扫过的面积都是相等的. 由扇形面积S= lr知半径长的对应的弧长短,由v=
lr知半径长的对应的弧长短,由v= 知行星离太阳较远时速率小,较近时速率大.即行星在近日点的速率大,远日点的速率小.故A错误、B正确.
知行星离太阳较远时速率小,较近时速率大.即行星在近日点的速率大,远日点的速率小.故A错误、B正确.
C、在a处速度方向与Oa垂直,即向心力指向A,而万有引力也是指向A,万有引力等于向心力.故C正确.
D、在b处的向心加速度与速度方向垂直指向O,用来改变速度的方向.但切向还有加速度,使得速度的大小在变小,即改变速度的大小.故b处的实际加速度方向不是指向O.根据牛顿第二定律,合力决定加速度,所以b处的加速度直线A.故D错误.
故选BC.
点评:考查了开普勒第二定律,再结合时间相等,面积相等,对应弧长求出平均速度.此题难度不大,属于基础题.

解答:解:A、B:根据开普勒第二定律,也称面积定律:在相等时间内,太阳和运动着的行星的连线所扫过的面积都是相等的. 由扇形面积S=
 lr知半径长的对应的弧长短,由v=
lr知半径长的对应的弧长短,由v= 知行星离太阳较远时速率小,较近时速率大.即行星在近日点的速率大,远日点的速率小.故A错误、B正确.
知行星离太阳较远时速率小,较近时速率大.即行星在近日点的速率大,远日点的速率小.故A错误、B正确.C、在a处速度方向与Oa垂直,即向心力指向A,而万有引力也是指向A,万有引力等于向心力.故C正确.
D、在b处的向心加速度与速度方向垂直指向O,用来改变速度的方向.但切向还有加速度,使得速度的大小在变小,即改变速度的大小.故b处的实际加速度方向不是指向O.根据牛顿第二定律,合力决定加速度,所以b处的加速度直线A.故D错误.
故选BC.
点评:考查了开普勒第二定律,再结合时间相等,面积相等,对应弧长求出平均速度.此题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
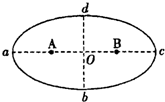 某行星绕太阳运动轨迹如图所示,图中A、B为椭圆轨迹的两个焦点,太阳位于A处,a为近日点,c为远日点,O为椭圆的几何中心,则行星( )
某行星绕太阳运动轨迹如图所示,图中A、B为椭圆轨迹的两个焦点,太阳位于A处,a为近日点,c为远日点,O为椭圆的几何中心,则行星( )