题目内容
(2004?南京三模)如图甲所示,A、B是一对平行放置的金属板,中心各有一个小孔P、Q,PQ连线垂直金属板,两板间距为d.现从P点处连续不断地有质量为 m、带电量为+q的带电粒子(重力不计),沿PQ方向放出,粒子的初速度可忽略不计.在t=0时刻开始在A、B间加上如图乙所示交变电压(A板电势高于B板电势时,电压为正),其电压大小为U、周期为T.带电粒子在A、B间运动过程中,粒子间相互作用力可忽略不计.

(1)如果只有在每个周期的0~
时间内放出的带电粒子才能从小孔Q中射出,则上述物理量之间应满足怎样的关系.
(2)如果各物理量满足(1)中的关系,求每个周期内从小孔Q中有粒子射出的时间与周期T的比值.

(1)如果只有在每个周期的0~
| T | 4 |
(2)如果各物理量满足(1)中的关系,求每个周期内从小孔Q中有粒子射出的时间与周期T的比值.
分析:(1)通过分析每个周期内带电粒子的运动情况,确定只有在每个周期的0~
时间内放出的带电粒子才能从小孔Q中射出时应满足的条件,根据牛顿第二定律和运动学公式求解各物理量之间应满足的关系.
(2)t=0时刻进入电场的粒子在电场中运动的时间为最短,由运动学公式求出最短时间.
| T |
| 4 |
(2)t=0时刻进入电场的粒子在电场中运动的时间为最短,由运动学公式求出最短时间.
解答:解:(1)在0→
时间内,进入A、B板间的粒子,在电场力的作用下,先向右做匀加速运动,在
→T时间内再向右做匀减速运动,且在0→
时间内,越迟进入A、B板间的粒子,其加速过程越短,减速运动过程也相应地缩短,当速度为零后,粒子会反向向左加速运动.由题意可知0→
时间内放出的粒子进入A、B板间,均能从Q孔射出,也就是说在
时刻进入A、B板间的粒子是能射出Q孔的临界状态.
粒子在
时刻进入A、B间电场时,先加速,后减速,由于粒子刚好离开电场,说明它离开电场的速度为零,由于加速和减速的对称性,故粒子的总位移为加速时位移的2倍,所以有
d=2×
a(
)2=
即 d2=
①
(2)若情形(1)中的关系式①成立,则t=0时刻进入电场的粒子在电场中运动的时间为最短(因只有加速过程),设最短时间为tx,则有
d=
a
②
在t=
时刻进入电场的粒子在t=
的时刻射出电场,所以有粒子飞出电场的时间为 △t=
-tx ③
由②③式得
=
④
答:
(1)各物理量之间应满足的关系是即d2=
.
(2)每个周期内从小孔Q中有粒子射出的时间与周期T的比值是
.
| T |
| 4 |
| T |
| 2 |
| T |
| 4 |
| T |
| 4 |
| T |
| 4 |
粒子在
| T |
| 4 |
d=2×
| 1 |
| 2 |
| T |
| 4 |
| qUT2 |
| 16md |
即 d2=
| qUT2 |
| 16m |
(2)若情形(1)中的关系式①成立,则t=0时刻进入电场的粒子在电场中运动的时间为最短(因只有加速过程),设最短时间为tx,则有
d=
| 1 |
| 2 |
| t | 2 x |
在t=
| T |
| 4 |
| 3T |
| 4 |
| 3T |
| 4 |
由②③式得
| △t |
| T |
3-
| ||
| 4 |
答:
(1)各物理量之间应满足的关系是即d2=
| qUT2 |
| 16m |
(2)每个周期内从小孔Q中有粒子射出的时间与周期T的比值是
3-
| ||
| 4 |
点评:本题关键是分析带电粒子的运动情况,确定出临界条件,运用牛顿第二定律和运动学规律结合进行求解.

练习册系列答案
相关题目
 (2004?南京三模)如图所示为光电管工作原理图,当有波长(均指真空中的波长,下同)为λ的光照射阴极板K时,电路中有光电流,则( )
(2004?南京三模)如图所示为光电管工作原理图,当有波长(均指真空中的波长,下同)为λ的光照射阴极板K时,电路中有光电流,则( ) (2004?南京三模)现有下列器材:电压表V1(量程3V,内阻约几千欧)、电压表V2(量程6V,内阻约几十千欧)、定值电阻R1(3.0kΩ)滑动变阻器R(0-5000Ω)、直流电源(约6V,内阻不计)开关及导线若干.某同学利用上述器材测量电压表V1的内阻值.
(2004?南京三模)现有下列器材:电压表V1(量程3V,内阻约几千欧)、电压表V2(量程6V,内阻约几十千欧)、定值电阻R1(3.0kΩ)滑动变阻器R(0-5000Ω)、直流电源(约6V,内阻不计)开关及导线若干.某同学利用上述器材测量电压表V1的内阻值.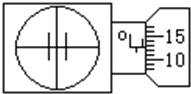 (2004?南京三模)在“用双缝干涉测光的波长”的实验中,测量头如图所示,调节分划板的位置,使分划板中心刻线对齐某亮条纹的中心,此时螺旋测微器的读数为
(2004?南京三模)在“用双缝干涉测光的波长”的实验中,测量头如图所示,调节分划板的位置,使分划板中心刻线对齐某亮条纹的中心,此时螺旋测微器的读数为