题目内容
5.如图1是“研究平抛物体运动”的实验装置图,通过描点可以画出平抛小球的运动轨迹.(1)以下是实验过程中的一些做法,其中合理的有ac.
A.安装斜槽轨道,一定要使其末端保持水平
b.每次小球必须静止释放,但初始位置可以任意选择
c.每次小球必须从同一高度由静止释放
d.为描出小球的运动轨迹,描绘的点最后可以用折线连接起来
(2)实验得到平抛小球的运动轨迹,在轨迹上取一些点,以平抛起点O为坐标原点,测量它们的水平坐标x和竖直坐标y,图2中y-x2图象能说明平抛小球运动轨迹为抛物线的是C.
(3)图3是某同学根据实验画出的平抛小球的运动轨迹,O为平抛的起点,在轨迹上任取三点A、B、C,测得A、B两点竖直坐标y1为5.0cm,y2为45.0cm,A、B两点水平间距△x为40.0cm,则平抛小球的初速度v0为2.0m/s,若C点的竖直坐标y3为60.0cm,则小球在C点的速度vC为4.0m/s(结果保留两位有效数字,g取10m/s2).

分析 (1)保证小球做平抛运动必须通过调节使斜槽的末端保持水平,因为要画同一运动的轨迹,必须每次释放小球的位置相同,且由静止释放,以保证获得相同的初速度,实验要求小球滚下时不能碰到木板平面,避免因摩擦而使运动轨迹改变,最后轨迹应连成平滑的曲线.(2)平抛运动竖直方向做自由落体运动,水平方向做匀速直线运动;联立求得两个方向间的位移关系可得出正确的图象.(3)根据平抛运动的处理方法,直方向做自由落体运动,水平方向做匀速直线运动即可求解.
解答 解:(1)a、通过调节使斜槽末端保持水平,是为了保证小球做平抛运动,故a正确;
bc、因为要画同一运动的轨迹,必须每次释放小球的位置相同,且由静止释放,以保证获得相同的初速度,故b错误,c正确;
d、用描点法描绘运动轨迹时,应将各点连成平滑的曲线,不能练成折线或者直线,故d错误.
故选:ac.
(2)物体在竖直方向做自由落体运动,y=$\frac{1}{2}$gt2;水平方向做匀速直线运动,x=vt;
联立可得:y=$\frac{g{x}^{2}}{2{v}_{0}^{2}}$,因初速度相同,故$\frac{g}{2{v}_{0}^{2}}$为常数,故y-x2应为正比例关系,故C正确,ABD错误.
故选:C.
(3)根据平抛运动的处理方法,竖直方向做自由落体运动,水平方向做匀速直线运动,
所以y1=$\frac{1}{2}$g${t}_{1}^{2}$ …①
y2=$\frac{1}{2}$g${t}_{2}^{2}$ …②
水平方向的速度,即平抛小球的初速度为v0=$\frac{△x}{△t}$…③
联立①②③代入数据解得:v0=2.0m/s
若C点的竖直坐标y3为60.0cm,则小球在C点的对应速度vC:据公式可得:${v}_{下}^{2}$=2gh,
所以v下=2$\sqrt{3}$m/s=3.5m/s
所以C点的速度为:vc=$\sqrt{12+4}$=4.0m/s
故答案为:(1)ac;(2)C;(3)2.0;4.0.
点评 解决平抛实验问题时,要特别注意实验的注意事项,在平抛运动的规律探究活动中不一定局限于课本实验的原理,要注重学生对探究原理的理解,提高解决问题的能力;灵活应用平抛运动的处理方法是解题的关键.

 一质量为m的物体,只受重力和另一恒力F作用,在竖直平面内沿直线从O点运动到A点,已知OA=1,与竖直方向的夹角为θ,如图所示,则下列说法错误的是( )
一质量为m的物体,只受重力和另一恒力F作用,在竖直平面内沿直线从O点运动到A点,已知OA=1,与竖直方向的夹角为θ,如图所示,则下列说法错误的是( )| A. | F的最小值为mgsinθ | |
| B. | 物体到达A的速度可能为$\sqrt{2glcosθ}$ | |
| C. | 若时F=mgtanθ,恒力F一定做正功 | |
| D. | 物体重力势能的减少量可能等于其动能的增加量 |
 如图所示,铁饼运动员奋力将质量为m的铁饼以初速度v0抛出,v0与水平面成α角,铁饼到达的最大高度为h,半径空气阻力和抛出点的高度,则运动员抛铁饼过程对铁饼做的功是( )
如图所示,铁饼运动员奋力将质量为m的铁饼以初速度v0抛出,v0与水平面成α角,铁饼到达的最大高度为h,半径空气阻力和抛出点的高度,则运动员抛铁饼过程对铁饼做的功是( )| A. | $\frac{1}{2}$mv02 | B. | mgh | C. | $\frac{1}{2}$mv02+mgh | D. | mv02+mgh |
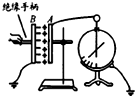 如图为“探究平行板电容器的电容与哪些因素有关”的装置图,已充电的平行板电容器的极板A与一静电计相连接,极板B接地,若极板B竖直向上移动少许,则电容器的电容减小,静电计指针偏角增大,电容器的电荷量几乎不变(填“增大”、“减小”或“几乎不变”)
如图为“探究平行板电容器的电容与哪些因素有关”的装置图,已充电的平行板电容器的极板A与一静电计相连接,极板B接地,若极板B竖直向上移动少许,则电容器的电容减小,静电计指针偏角增大,电容器的电荷量几乎不变(填“增大”、“减小”或“几乎不变”) 如图所示,在光滑的水平地面上,质量为mA=1.0kg的小球A以vA=4.0m/s的速度,某时刻与静止的小球B发生对心碰撞,碰撞后A球以vA=1.0m/s的速度继续向右运动,B球以vB=3.0m/s的速度也向右运动.
如图所示,在光滑的水平地面上,质量为mA=1.0kg的小球A以vA=4.0m/s的速度,某时刻与静止的小球B发生对心碰撞,碰撞后A球以vA=1.0m/s的速度继续向右运动,B球以vB=3.0m/s的速度也向右运动. 如图所示,用U形管和细管连接的玻璃烧瓶A和橡胶气囊B内都充有理想气体,A浸泡在温度为27℃水槽中,U形管右侧水银柱比左侧高h=40cm.现挤压气囊B,使其体积变为原来的$\frac{2}{3}$,此时U形管两侧的水银柱等高.已知挤压过程中气囊B温度保持不变,U形管和细管的体积远小于A、B的容积,变化过程中烧瓶A中气体体积可认为不变.
如图所示,用U形管和细管连接的玻璃烧瓶A和橡胶气囊B内都充有理想气体,A浸泡在温度为27℃水槽中,U形管右侧水银柱比左侧高h=40cm.现挤压气囊B,使其体积变为原来的$\frac{2}{3}$,此时U形管两侧的水银柱等高.已知挤压过程中气囊B温度保持不变,U形管和细管的体积远小于A、B的容积,变化过程中烧瓶A中气体体积可认为不变. 如图所示,水平放置的平行金属导轨cdef,相距l=0.50m,左端接一阻值为R=0.20Ω的电阻,磁感应强度B=0.40T的匀强磁场方向垂直于导轨平面,导体棒ab放在导轨上且与cd、ef垂直,并能无摩擦地沿导轨滑动且接触良好,导体棒的电阻r=0.10Ω,导体棒的长度亦为l=0.50m,导轨电阻可忽略不计,当ab棒以v=3.0m/s的速度水平向右匀速滑动时,求
如图所示,水平放置的平行金属导轨cdef,相距l=0.50m,左端接一阻值为R=0.20Ω的电阻,磁感应强度B=0.40T的匀强磁场方向垂直于导轨平面,导体棒ab放在导轨上且与cd、ef垂直,并能无摩擦地沿导轨滑动且接触良好,导体棒的电阻r=0.10Ω,导体棒的长度亦为l=0.50m,导轨电阻可忽略不计,当ab棒以v=3.0m/s的速度水平向右匀速滑动时,求 如图所示,AB为一段弯曲轨道,固定在水平桌面上,与水平桌面相切于A点,B点距桌面的高度为h=0.6m,A、B两点间的水平距离为L=0.8m,轨道边缘B处有一轻、小定滑轮,一根轻绳两端系着质量分别为m1与m2的物体P、Q,挂在定滑轮两边,P、Q可视为质点,且m1=2.0kg,m2=0.4kg.开始时P、Q均静止,P紧靠B点,P释放后沿弯曲轨道向下运动,运动到A点时轻绳突然断开,断开后P沿水平桌面滑行距离x=1.25m停止.已知P与水平桌面间的动摩擦因数μ=0.25,g取10m/s2.求:
如图所示,AB为一段弯曲轨道,固定在水平桌面上,与水平桌面相切于A点,B点距桌面的高度为h=0.6m,A、B两点间的水平距离为L=0.8m,轨道边缘B处有一轻、小定滑轮,一根轻绳两端系着质量分别为m1与m2的物体P、Q,挂在定滑轮两边,P、Q可视为质点,且m1=2.0kg,m2=0.4kg.开始时P、Q均静止,P紧靠B点,P释放后沿弯曲轨道向下运动,运动到A点时轻绳突然断开,断开后P沿水平桌面滑行距离x=1.25m停止.已知P与水平桌面间的动摩擦因数μ=0.25,g取10m/s2.求: