Question

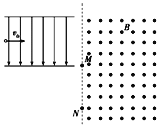
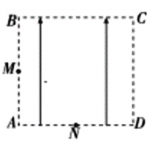
【题目】如图所示，匀强电场分布在边长为L的正方形区域ABCD内，M、N分别为AB和AD的中点，一个初速度为v0，质量为m的带负电粒子q沿纸面射入电场．带电粒子的重力不计．

（1）如果带电粒子从M点垂直电场方向进入电场后，恰好从D点离开电场，求匀强电场的电场强度E和带电粒子从D点离开电场时的动能Ek1.

（2）若带电粒子从N点垂直BC方向射入电场，它在电场中的运动时间t是多少？离开电场时的动能Ek2为多大？

Answer 1

【答案】（1）.（2）.

【解析】

（1）带电粒子从M点垂直电场线进入电场后做类平抛运动．

水平方向：

①

竖直方向：

②

联立①②得

.

带电粒子从M点进入电场后，从D点出来，电场力做的功

③

由动能定理得

所以

.

（2）带电粒子从N点进入电场后做匀减速直线运动，设速度减到0这一过程的位移为x，由动能定理：

④

由③④得

.

当粒子速度减至0后沿原路返回，从N点射出，由于整个过程电场力做的功为0，则

根据动能定理有

.

则，即粒子离开电场时的速度大小不变，由牛顿第二定律得

.

由运动学规律得

得

.