题目内容
【题目】传送带被广泛应用于各行各业。由于不同的物体与传送带之间的动摩擦因数不同,物体在传送带上的运动情况也有所不同。如图所示,一倾斜放置的传送带与水平面的倾角θ=370, 在电动机的带动下以v=2m/s的速率顺时针方向匀速运行。M、N为传送带的两个端点,MN两点间的距离L=7m。N端有一离传送带很近的挡板P可将传送 带上的物块挡住。在传送带上的O处先后由静止释放金属块A和木块B,金属块与木块质量均为1kg,且均可视为质点,OM间距离L=3m。 sin37°=0.6,cos37°=0.8,g取10m/s2。传送带与轮子间无相对滑动,不计轮轴处的摩擦。
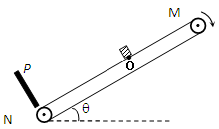
(1)金属块A由静止释放后沿传送带向上运动,经过2s到达M端,求金属块与传送带间的动摩擦因数μ1。
(2)木块B由静止释放后沿传送带向下运动,并与挡板P发生碰撞。已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,木块B与传送带间的动摩擦因数μ2=0.5。求:与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离;
【答案】(1)1(2)1.6m
【解析】
试题分析:(1)金属块A在传送带方向上受摩擦力和重力的下滑分力,先做匀加速运动,并设其速度能达到传送带的速度v=2m/s,然后做匀速运动,达到M点.
金属块由O运动到M有 L=![]() at12+vt2
at12+vt2
即 ![]() at12+2t2=3 ①
at12+2t2=3 ①
且 t1+t2=t
即 t1+t2=2 ②
v=at1
即 2=at1 ③
根据牛顿第二定律有 μ1mgcos370mgsin370=ma ④
由①②③式解得 t1=1s<t=2s 符合题设要求,加速度a=2m/s2
由④式解得金属块与传送带间的动摩擦因数μ1=1
(2)由静止释放后,木块B沿传送带向下做匀加速运动,其加速度为a1,运动距离LON=4m,第一次与P碰撞前的速度为v1
a1=gsinθ-μgcosθ=2m/s2
![]()
与挡板P第一次碰撞后,木块B以速度v1被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s1;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s2.
a2=gsinθ+μgcosθ=10m/s2,
![]()
![]()
因此与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离s=s1+s2=1.6m

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案