题目内容
5.质量为m的小球被系在轻绳一端,在竖直平面内做半径为R的圆周运动,运动过程中小球受到空气阻力作用,设某一时刻小球通过轨道的最低点.此时绳子的张力为7mg,在此后小球继续做圆周运动,经过半个圆周恰好能通过最高点,则在此过程中小球克服空气阻力作的功是( )| A. | $\frac{1}{4}$mgR | B. | $\frac{1}{3}$mgR | C. | $\frac{1}{2}$mgR | D. | mgR |
分析 圆周运动在最高点和最低点沿径向的合力提供向心力,根据牛顿第二定律求出最高点和最低点的速度,再根据动能定理求出此过程中小球克服空气阻力所做的功.
解答 解:小球在最低点,由牛顿第二定律有:F-mg=m$\frac{{v}_{1}^{2}}{R}$
据题 F=7mg
最高点时,由于小球恰好能通过最高点,所以有:mg=m$\frac{{v}_{2}^{2}}{R}$
小球选取从最低点到最高点作为过程,由动能定理可得:
-mg•2R-Wf=$\frac{1}{2}$m${v}_{2}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$
由以上三式可得:Wf=$\frac{1}{2}$mgR
故选:C
点评 由绳子的拉力可求出最低点速度,由恰好能通过最高点求出最高点速度,这都是题目中隐含条件.同时在运用动能定理时,明确初动能与末动能,及过程中哪些力做功,做正功还是负功.

练习册系列答案
相关题目
15.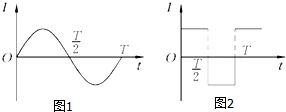 两个相同的电阻分别通以正弦式波形的交流电和方波形的交流电,两种交流电电流的最大值相等,波形如图所示,在简谐波形交流电的一个周期内,简谐波形的交流电在电阻上产生的电热Q1与方波形交流电在电阻上产生的电热Q2之比$\frac{{Q}_{1}}{{Q}_{2}}$等于( )
两个相同的电阻分别通以正弦式波形的交流电和方波形的交流电,两种交流电电流的最大值相等,波形如图所示,在简谐波形交流电的一个周期内,简谐波形的交流电在电阻上产生的电热Q1与方波形交流电在电阻上产生的电热Q2之比$\frac{{Q}_{1}}{{Q}_{2}}$等于( )
 两个相同的电阻分别通以正弦式波形的交流电和方波形的交流电,两种交流电电流的最大值相等,波形如图所示,在简谐波形交流电的一个周期内,简谐波形的交流电在电阻上产生的电热Q1与方波形交流电在电阻上产生的电热Q2之比$\frac{{Q}_{1}}{{Q}_{2}}$等于( )
两个相同的电阻分别通以正弦式波形的交流电和方波形的交流电,两种交流电电流的最大值相等,波形如图所示,在简谐波形交流电的一个周期内,简谐波形的交流电在电阻上产生的电热Q1与方波形交流电在电阻上产生的电热Q2之比$\frac{{Q}_{1}}{{Q}_{2}}$等于( )| A. | 3:1 | B. | 1:2 | C. | 2:1 | D. | 4:3 |
16. 如图1所示,一个带正电的物块m,由静止开始从斜面上A点下滑,滑到水平面BC上的D点停下来.已知物块与斜面及水平面间的动摩擦因数相同,且不计物块经过B处时的机械能损失,现在ABC所在空间加竖直向下的匀强电场,如图2,第二次让物块m从A点由静止开始下滑,结果物块在水平面上的D′点停下.后又撤去电场,在ABC所在空间加水平向里的匀强磁场,如图3,再次让物块从A点由静止开始下滑,结果物块沿斜面滑下并在水平面上的D″点停下来.则下列说法中正确的是( )
如图1所示,一个带正电的物块m,由静止开始从斜面上A点下滑,滑到水平面BC上的D点停下来.已知物块与斜面及水平面间的动摩擦因数相同,且不计物块经过B处时的机械能损失,现在ABC所在空间加竖直向下的匀强电场,如图2,第二次让物块m从A点由静止开始下滑,结果物块在水平面上的D′点停下.后又撤去电场,在ABC所在空间加水平向里的匀强磁场,如图3,再次让物块从A点由静止开始下滑,结果物块沿斜面滑下并在水平面上的D″点停下来.则下列说法中正确的是( )
 如图1所示,一个带正电的物块m,由静止开始从斜面上A点下滑,滑到水平面BC上的D点停下来.已知物块与斜面及水平面间的动摩擦因数相同,且不计物块经过B处时的机械能损失,现在ABC所在空间加竖直向下的匀强电场,如图2,第二次让物块m从A点由静止开始下滑,结果物块在水平面上的D′点停下.后又撤去电场,在ABC所在空间加水平向里的匀强磁场,如图3,再次让物块从A点由静止开始下滑,结果物块沿斜面滑下并在水平面上的D″点停下来.则下列说法中正确的是( )
如图1所示,一个带正电的物块m,由静止开始从斜面上A点下滑,滑到水平面BC上的D点停下来.已知物块与斜面及水平面间的动摩擦因数相同,且不计物块经过B处时的机械能损失,现在ABC所在空间加竖直向下的匀强电场,如图2,第二次让物块m从A点由静止开始下滑,结果物块在水平面上的D′点停下.后又撤去电场,在ABC所在空间加水平向里的匀强磁场,如图3,再次让物块从A点由静止开始下滑,结果物块沿斜面滑下并在水平面上的D″点停下来.则下列说法中正确的是( )| A. | D′点一定在D点左侧 | B. | D′点一定与D点重合 | ||
| C. | D″点一定在D点右侧 | D. | D″点一定与D点重合 |
20. 如图所示,质量为m的物体在外力作用下从a点分别沿abc和adc轨迹运动到其左下方的c点.已知a点与c点间的高度差为h,物体两次运动的时间均为t,重力加速度为g,则以下说法中正确的是( )
如图所示,质量为m的物体在外力作用下从a点分别沿abc和adc轨迹运动到其左下方的c点.已知a点与c点间的高度差为h,物体两次运动的时间均为t,重力加速度为g,则以下说法中正确的是( )
 如图所示,质量为m的物体在外力作用下从a点分别沿abc和adc轨迹运动到其左下方的c点.已知a点与c点间的高度差为h,物体两次运动的时间均为t,重力加速度为g,则以下说法中正确的是( )
如图所示,质量为m的物体在外力作用下从a点分别沿abc和adc轨迹运动到其左下方的c点.已知a点与c点间的高度差为h,物体两次运动的时间均为t,重力加速度为g,则以下说法中正确的是( )| A. | 物体沿abc轨迹运动时,重力势能先减小后增大 | |
| B. | 两次运动过程中重力做功的平均功率相等 | |
| C. | 物体沿abc轨迹运动时,重力做功大于mgh | |
| D. | 物体沿adc轨迹运动时,重力做功大于mgh |
10.用绿光做双缝干涉实验,在光屏上呈现出明、暗相间的条纹,相邻两条明条纹间的距离为△x,下列说法中正确的是( )
| A. | 如果增大单缝到双缝间的距离,△x将增大 | |
| B. | 如果增大双缝之间的距离,△x将增大 | |
| C. | 如果增大双缝到光屏之间的距离,△x将增大 | |
| D. | 如果将绿光换成紫光,△x将增大 |
17.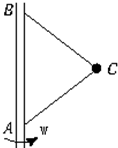 如图所示,小球C用两根长度相等,不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述正确的是( )
如图所示,小球C用两根长度相等,不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述正确的是( )
 如图所示,小球C用两根长度相等,不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述正确的是( )
如图所示,小球C用两根长度相等,不可伸长的细线系在竖直杆上,它们随竖直杆转动,在转动角速度变化时,下列关于细线上的力的叙述正确的是( )| A. | 角速度只有超过某一值时,细线AC才会对小球C有拉力作用 | |
| B. | 细线BC的拉力随角速度的增大而增大 | |
| C. | 不论角速度如何变化,细线BC的拉力总大于细线AC的拉力 | |
| D. | 当角速度增大到某一值时,总会出现细线AC的拉力大于细线BC的拉力 |
15.下列有关物理学史,不符合事实的是( )
| A. | 麦克斯韦建立了电磁场理论并预言了电磁波的存在 | |
| B. | 伽利略认为,力学规律在任何惯性系中都是相同的 | |
| C. | 赫兹首先捕捉到了电磁波 | |
| D. | 牛顿发现了单摆周期公式 |
 如图所示,匀强磁场的磁感应强度B=2.0T,并指向x轴正方向,若ab=40cm,bc=30cm,ae=50cm,试求通过面积S1(abcd)、S2(befc)和S3(aefd)的磁通量分别为φ1、φ2、φ3分别是多少?
如图所示,匀强磁场的磁感应强度B=2.0T,并指向x轴正方向,若ab=40cm,bc=30cm,ae=50cm,试求通过面积S1(abcd)、S2(befc)和S3(aefd)的磁通量分别为φ1、φ2、φ3分别是多少? 在“用单摆测定重力加速度”的实验中,测得单摆摆角小于5°,完成n全振动的时间为t,用毫米刻度尺测得摆线长为L,用螺旋测微器测得摆球的直径为d.
在“用单摆测定重力加速度”的实验中,测得单摆摆角小于5°,完成n全振动的时间为t,用毫米刻度尺测得摆线长为L,用螺旋测微器测得摆球的直径为d.