题目内容
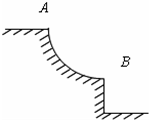 如图所示,圆弧轨道AB在竖直平面内,在B点,轨道的切线是水平的,一小球由圆弧轨道上的某点从静止开始下滑,不计任何阻力.设小球刚到达B点时的加速度为a1,刚滑过B点时的加速度为a2,则( )
如图所示,圆弧轨道AB在竖直平面内,在B点,轨道的切线是水平的,一小球由圆弧轨道上的某点从静止开始下滑,不计任何阻力.设小球刚到达B点时的加速度为a1,刚滑过B点时的加速度为a2,则( )分析:质点刚要到达B点时,受重力和支持力,两个力的合力提供向心力,根据牛顿第二定律求出加速度大小.滑过B点时所受的合力为重力,根据牛顿第二定律求出加速度的大小.
解答:解:质点刚要到达B点时,有:F合=m
=ma1.根据动能定理得,mgR=
mv2.联立两式,a1=2g,方向竖直向上.
滑过B点时所受的合力为重力,根据牛顿第二定律得,a2=
=g,方向竖直向下.
故选D.
| v2 |
| R |
| 1 |
| 2 |
滑过B点时所受的合力为重力,根据牛顿第二定律得,a2=
| mg |
| m |
故选D.
点评:解决本题的关键知道质点刚要到达B点时,受重力和支持力,两个力的合力提供向心力.滑过B点时所受的合力为重力.

练习册系列答案
相关题目
 如图所示,圆弧轨道AB是在竖直平面内的
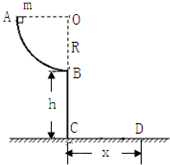
如图所示,圆弧轨道AB是在竖直平面内的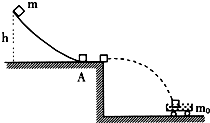 (2006?和平区模拟)质量为m的小滑块自圆弧轨道上端由静止滑下,如图所示,圆弧轨道半径为R,高度为h.A点为弧形轨道与水平桌面的平滑接点.滑块离开桌面后恰好落人静止在水平面上的装满沙的总质量为m0的小车中,桌面到小车上沙平面的高度也是h.木块落人车内与沙面接触直到相对静止经过的较短时间为t.试回答下列问题.(所有接触面的摩擦不计,重力加速度g已知,小车高度不计)
(2006?和平区模拟)质量为m的小滑块自圆弧轨道上端由静止滑下,如图所示,圆弧轨道半径为R,高度为h.A点为弧形轨道与水平桌面的平滑接点.滑块离开桌面后恰好落人静止在水平面上的装满沙的总质量为m0的小车中,桌面到小车上沙平面的高度也是h.木块落人车内与沙面接触直到相对静止经过的较短时间为t.试回答下列问题.(所有接触面的摩擦不计,重力加速度g已知,小车高度不计)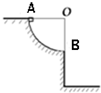 如图所示,圆弧轨道AB是在竖直平面内的
如图所示,圆弧轨道AB是在竖直平面内的 如图所示,圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧拴接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B-超运动但与B不粘连.求:
如图所示,圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧拴接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B-超运动但与B不粘连.求: