题目内容
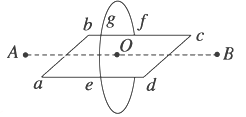
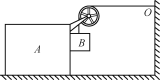
【题目】如图甲所示,质量m=1.0×l0-3kg的“![]() ”形金属细框竖直放置在两水银槽中,“
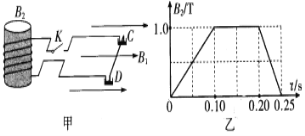
”形金属细框竖直放置在两水银槽中,“![]() ”形框的水平细杆CD长l=0.20m,处于磁感应强度大小B1=1.0T、方向水平向右的匀强磁场中.有一匝数n=150匝、面积S=2.0×l0-3m2的线圈通过开关K与两水银槽相连。线圈处于与线圈平面垂直、沿竖直方向的匀强磁场中,其磁感应强度B2随时间t变化的关系如图乙所示.t=0.24s时闭合开关K,瞬间细框跳起(细框跳起瞬间安培力远大于重力),跳起的最大高度h=0.20m.不计空气阻力和水银的黏滞作用,重力加速度g=10m/s2,下列说法正确的是
”形框的水平细杆CD长l=0.20m,处于磁感应强度大小B1=1.0T、方向水平向右的匀强磁场中.有一匝数n=150匝、面积S=2.0×l0-3m2的线圈通过开关K与两水银槽相连。线圈处于与线圈平面垂直、沿竖直方向的匀强磁场中,其磁感应强度B2随时间t变化的关系如图乙所示.t=0.24s时闭合开关K,瞬间细框跳起(细框跳起瞬间安培力远大于重力),跳起的最大高度h=0.20m.不计空气阻力和水银的黏滞作用,重力加速度g=10m/s2,下列说法正确的是
A. 0 -0.10s内线圈中的感应电动势大小为3V
B. 磁感应强度B2的方向竖直向下
C. 开关K闭合瞬间,CD中的电流方向由C到D
D. 开关K闭合瞬间,通过细杆CD的电荷量为0.03C
【答案】AC
【解析】
由法拉第电磁感应定律可以求出感应电动势。由左手定则可以判断出感应电流方向,然后应用安培定则判断出感应电流磁场的方向,最后应用楞次定律判断磁感应强度的方向。依据左手定则,结合细框跳起瞬间安培力远大于重力,即可求解;细框向上做竖直上抛运动,应用竖直上抛运动规律可以求出细框获得的速度,由动量定理求出细框受到的安培力,然后由电流定义式的变形公式求出电荷量。
由图示图象可知,0~0.10s内:△Φ=△BS=(1-0)×2.0×10-3=2.0×10-3Wb,0~0.10s线圈中的感应电动势大小:![]() ,故A正确;细杆CD所受安培力方向竖直向上,由左手定律可知,电流方向为:C→D;由安培定则可知感应电流的磁场方向竖直向上,由图示图象可知,在0.2-0.25s内穿过线圈的磁通量减少,由楞次定律可知,磁感应强度B2方向:竖直向上,故B错误,C正确;对细框,由动量定理得:B1Il△t=mv-0,细框竖直向上做竖直上抛运动:v2=2gh,电荷量:Q=I△t,解得:
,故A正确;细杆CD所受安培力方向竖直向上,由左手定律可知,电流方向为:C→D;由安培定则可知感应电流的磁场方向竖直向上,由图示图象可知,在0.2-0.25s内穿过线圈的磁通量减少,由楞次定律可知,磁感应强度B2方向:竖直向上,故B错误,C正确;对细框,由动量定理得:B1Il△t=mv-0,细框竖直向上做竖直上抛运动:v2=2gh,电荷量:Q=I△t,解得:![]() ,故D错误;故选AC。
,故D错误;故选AC。