题目内容
如图a所示,水平面上质量相等的两木块A、B,用一轻弹簧相连,这个系统处于平衡状态,现用一竖直向上的力F拉动木块A,使木块A向上做匀加速直线运动(如图b),研究从力F刚作用在木块A瞬间到木块B刚离开地面瞬间的这一过程,并选定该过程中木块A的起点位置为坐标原点,则下面图中能正确表示力F和木块A的位移x之间关系的图是( )
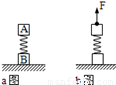 A.
A.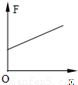 B.
B.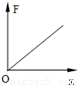 C.
C.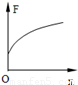 D.
D.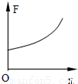
【答案】
A
【解析】
试题分析:由于开始时系统处于平衡状态,因此弹簧亦应处于原长状态,因此在B未离开地面之前,木块A的位移即对应了弹簧的伸长量x,对木块A,受重力mg、弹簧弹力kx、竖直向上的拉力F作用,根据牛顿第二定律有:F-mg-kx=ma,解得:F=kx+m(g+a),即F与x呈一次函数关系,且纵截距m(g+a)>0,故选项A正确。
考点:本题主要考查了牛顿第二定律的应用,以及对图象的理解与应用问题,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013?顺义区一模)如图a所示,水平面上质量相等的两木块A、B,用轻弹簧相连接,这个系统处于平衡状态.现用一竖直向上的力F拉动木块A,使木块A向上做匀加速直线运动(如图b),研究从力F刚作用在木块A瞬间到木块B刚离开地面瞬间的这一过程,并选定该过程中木块A的起点位置为座标原点.则下面图中能正确表示力F和木块A的位移x之间关系的图是( )
(2013?顺义区一模)如图a所示,水平面上质量相等的两木块A、B,用轻弹簧相连接,这个系统处于平衡状态.现用一竖直向上的力F拉动木块A,使木块A向上做匀加速直线运动(如图b),研究从力F刚作用在木块A瞬间到木块B刚离开地面瞬间的这一过程,并选定该过程中木块A的起点位置为座标原点.则下面图中能正确表示力F和木块A的位移x之间关系的图是( ) 如图a所示,水平面上有质量相等的两个木块A、B用一根轻弹簧相连接,整个系统处于平衡状态.现用一个竖直向上的力F拉动木块A,使木块A向上做匀加速直线运动,如图b所示.研究从力F刚作用在木块A上时到木块B刚离开地面时这个过程,并且选定这个过程中木块A的起始位置为坐标原点,则下列图象中可以表示力F和木块A的位移x之间关系的是( )
如图a所示,水平面上有质量相等的两个木块A、B用一根轻弹簧相连接,整个系统处于平衡状态.现用一个竖直向上的力F拉动木块A,使木块A向上做匀加速直线运动,如图b所示.研究从力F刚作用在木块A上时到木块B刚离开地面时这个过程,并且选定这个过程中木块A的起始位置为坐标原点,则下列图象中可以表示力F和木块A的位移x之间关系的是( )









