题目内容
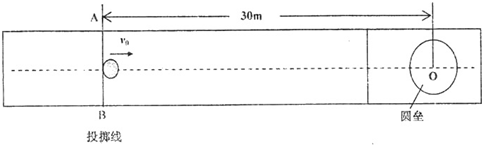
(2011?湖州模拟)冰壶比赛是在水平冰面上进行的体育项目,比赛场地示意如图所示.比赛时,运动员在投掷线AB处让冰壶以一定的初速度滑出,使冰壶的停止位置尽量靠近距离投掷线30m远的O点.为使冰壶滑行得更远,运动员可以用毛刷擦冰壶运行前方的冰面,使冰壶与冰面间的动摩擦因数减小.设冰壶与冰面间的动摩擦因数为μ1=0.008,用毛刷擦冰面后摩擦因数减少至μ2=0.004.在某次比赛中,运动员使冰壶C在投掷线中点处以v0=2m/s的速度沿虚线滑出.(g取10m/s2)
(1)若不用毛刷擦冰面,则冰壶停止的位置距离O点多远?
(2)为使冰壶C能够沿虚线恰好到达O点,运动员用毛刷擦冰面的长度应为多少?
(1)若不用毛刷擦冰面,则冰壶停止的位置距离O点多远?
(2)为使冰壶C能够沿虚线恰好到达O点,运动员用毛刷擦冰面的长度应为多少?

分析:对冰壶受力分析,运用动能定理研究滑动的过程求出位移,也可以运用牛顿第二定律求出冰壶的加速度,在运用运动学公式求出位移.
为使冰壶C能够沿虚线恰好到达O点,也就是说到达O点的速度为0.我们可以设冰壶在未被毛刷擦过的冰面上滑行的距离,
再运用动能定理研究整个过程,解出未知量.
为使冰壶C能够沿虚线恰好到达O点,也就是说到达O点的速度为0.我们可以设冰壶在未被毛刷擦过的冰面上滑行的距离,
再运用动能定理研究整个过程,解出未知量.
解答:解(1)运用动能定理研究冰壶滑出到停止这个过程:
-μ1mgs=0-
mv02
s=
=25m
30m-25m=5m
所以冰壶停止的位置距离O点5m.
(2)设冰壶在未被毛刷擦过的冰面上滑行的距离是s1,所受摩擦力的大小f1,在被毛刷擦过的冰面上滑行的距离s2,所受摩擦力的大小f2.则有
s1+s2=L ①(L为投掷线到圆心的距离)
f1=μ1mg ②f2=μ2mg ③
由功能关系,得-f1s1+(-f2s2)=0-
mv02
联立以上各式,解得 s2=
代入数据得 s2=10m
答:(1)冰壶停止的位置距离O点5m;
(2)运动员用毛刷擦冰面的长度应为10m.
-μ1mgs=0-
| 1 |
| 2 |
s=
| ||
| 2μ1g |
30m-25m=5m
所以冰壶停止的位置距离O点5m.
(2)设冰壶在未被毛刷擦过的冰面上滑行的距离是s1,所受摩擦力的大小f1,在被毛刷擦过的冰面上滑行的距离s2,所受摩擦力的大小f2.则有
s1+s2=L ①(L为投掷线到圆心的距离)
f1=μ1mg ②f2=μ2mg ③
由功能关系,得-f1s1+(-f2s2)=0-
| 1 |
| 2 |
联立以上各式,解得 s2=
2μ1gL-
| ||
| 2g(μ1-μ2) |
代入数据得 s2=10m
答:(1)冰壶停止的位置距离O点5m;
(2)运动员用毛刷擦冰面的长度应为10m.
点评:该题可以运用牛顿第二定律结合运动学公式求解,也可以运用动能定理求解,我们可以去比较哪个更简便.
运用动能定理时要注意过程中各力做功的求解.
运用动能定理时要注意过程中各力做功的求解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 (2011?湖州模拟)如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.滑杆MN垂直于导轨并可在导轨上滑动.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,绳处于拉直状态.现若从静止开始释放物块,用i表示回路中的感应电流,g表示重力加速度,则在物块下落过程中物块的速度可能( )
(2011?湖州模拟)如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.滑杆MN垂直于导轨并可在导轨上滑动.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,绳处于拉直状态.现若从静止开始释放物块,用i表示回路中的感应电流,g表示重力加速度,则在物块下落过程中物块的速度可能( )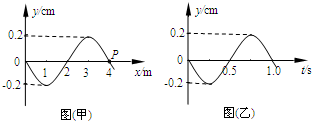 (2011?湖州模拟)一列横波在x轴上传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中质点P的振动图象.对该波的传播方向和传播波速度的说法正确的是( )
(2011?湖州模拟)一列横波在x轴上传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中质点P的振动图象.对该波的传播方向和传播波速度的说法正确的是( ) (2011?湖州模拟)如图所示匀强电场E的区域内,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心、半径为R的球面上的点,o、a、e、c、f点共面且与电场平行,o、b、e、d、f点共面且与电场垂直,则下列说法中正确的是( )
(2011?湖州模拟)如图所示匀强电场E的区域内,在O点处放置一点电荷+Q,a、b、c、d、e、f为以O点为球心、半径为R的球面上的点,o、a、e、c、f点共面且与电场平行,o、b、e、d、f点共面且与电场垂直,则下列说法中正确的是( )