题目内容
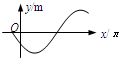 在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=25cos(kx+
在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=25cos(kx+| 2 |
| 3 |
分析:环在运动的过程中,机械能守恒,根据曲线方程可以确定环的位置,即环的高度的大小,再根据机械能守恒可以求得环的速度的大小和小环在x轴方向能运动的最远的位置.
解答:解:AB、光滑小环在沿金属杆运动的过程中,只有重力做功,机械能守恒,由曲线方程知,环在x=0处的y坐标是-
m,在x=
时,y=2.5cos(kx+
π)=-2.5 m
选y=0处为零势能参考平面,则有:
mv02+mg(-
)=
mv2+mg(-2.5)
解得:v=5
m/s,故A正确,B错误
CD、当环运动到最高点时,速度为零,
同理有:
mv02+mg(-
)=0+mgy
解得y=0,即:kx+
=π+
该小环在x轴方向最远能运动到x=
m,故C错误,D正确
故选AD
| 2.5 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
选y=0处为零势能参考平面,则有:
| 1 |
| 2 |
| 2.5 |
| 2 |
| 1 |
| 2 |
解得:v=5
| 2 |
CD、当环运动到最高点时,速度为零,
同理有:
| 1 |
| 2 |
| 2.5 |
| 2 |
解得y=0,即:kx+
| 2π |
| 3 |
| π |
| 2 |
该小环在x轴方向最远能运动到x=
| 5π |
| 6 |
故选AD
点评:本题和数学的上的方程结合起来,根据方程来确定物体的位置,从而利用机械能守恒来解题,题目新颖,是个好题.

练习册系列答案
相关题目

 如图,两根长度分别为L1和L2的光滑杆AB和BC在B点垂直焊接,当按图示方式固定在竖直平面内时,将一滑环从B点由静止释放,分别沿BA和BC滑到杆的底端经历的时间相同,则这段时间为( )
如图,两根长度分别为L1和L2的光滑杆AB和BC在B点垂直焊接,当按图示方式固定在竖直平面内时,将一滑环从B点由静止释放,分别沿BA和BC滑到杆的底端经历的时间相同,则这段时间为( ) B.
B.
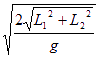 D.
D.