题目内容
如图甲所示,质量m=2 kg的物体在水平面上向右做直线运动。过a点时给物体作用一个水平向左的恒力F并开始计时,选水平向右为速度的正方向,通过速度传感器测出物体的瞬时速度,所得v-t图象如图乙所示。取重力加速度g=10 m/s2。求:
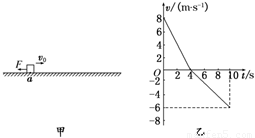
(1)力F的大小和物体与水平面间的动摩擦因数μ;
(2)10 s末物体离a点的距离。
【答案】
(1)F=3 N μ=0.05(2)物体在a点以左2m处
【解析】
试题分析:(1)设物体向右做匀减速直线运动的加速度为a1,则由v-t图得a1=2 m/s2①
根据牛顿第二定律,有F+μmg=ma1②
设物体向左做匀加速直线运动的加速度为a2,则由v-t图得
a2=1 m/s2③
根据牛顿第二定律,有F-μmg=ma2④
解①②③④得:F=3 N μ=0.05
(2)设10 s末物体离a点的距离为d,d应为v-t图与横轴所围的面积,则:d= ×4×8 m-
×4×8 m- ×6×6 m=-2 m,负号表示物体在a点以左。
×6×6 m=-2 m,负号表示物体在a点以左。
考点:此题考查运动图像及牛顿第二定律的应用问题。

练习册系列答案
相关题目
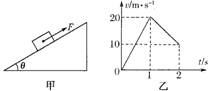
如图甲所示,质量m=1.0 kg的物体置于倾角θ=37º的固定粗糙斜面上,t=0时对物体施以平行于斜面向上的拉力F,t1=1 s时撤去拉力,物体运动的部分v-t图象如图乙所示。设斜面足够长,物体所受最大静摩擦力与滑动摩擦力大小相等,则下列说法正确的是(sin37º=0.6,cos37º=0.8,g取10 m/s2)
| A.拉力F的大小为20 N |
| B.物体运动到最高点的时间为3 s |
| C.0~1 s内克服重力做功的平均功率为100 W |
| D.t=4 s时物体的速度大小为10 m/s |