题目内容
12. 如图所示,位于水平面内间距为L的光滑平行“U”型导轨,置于磁感应强度大小为B的匀强磁场中,磁场方向垂直于导轨所在平面,一质量为m、长为L的直导体棒两端放在导轨上,并与之良好接触.已知导体棒的电阻为r,导轨的电阻忽略不计.从t=0时刻起,导棱在平行于“U”型导轨的水平向右的拉力作用下,从导轨左端由静止开始做加速度为a的匀加速动动.求
如图所示,位于水平面内间距为L的光滑平行“U”型导轨,置于磁感应强度大小为B的匀强磁场中,磁场方向垂直于导轨所在平面,一质量为m、长为L的直导体棒两端放在导轨上,并与之良好接触.已知导体棒的电阻为r,导轨的电阻忽略不计.从t=0时刻起,导棱在平行于“U”型导轨的水平向右的拉力作用下,从导轨左端由静止开始做加速度为a的匀加速动动.求(1)t时该导体棒中的电流;
(2)t时刻导体棒中水平向右的拉力;
(3)t时刻回路的电功率.
分析 (1)导体棒由静止开始做匀加速运动,t时刻速度为v=at,产生的感应电动势E=BLv,由欧姆定律即可求得电流;
(2)由牛顿第二定律可求得拉力;
(3)由电功率公式P=I2R求解此时电路中的电功率..
解答 解:(1)导体棒由静止开始做匀加速运动,在t时刻导体棒的速度为:
v=at
位移为:x=$\frac{1}{2}$at2
导体棒切割磁感线产生的感应电动势为:E=BLv
由闭合电路欧姆定律知,导体棒中的电流为:I=$\frac{E}{R}$=$\frac{BLat}{R}$;
(2)由牛顿第二定律可得:
F-BIL=ma;
解得:F=ma+$\frac{{B}^{2}{L}^{2}at}{R}$;
(3)回路中的电功率为:P=I2R=$\frac{{B}^{2}{L}^{2}{a}^{2}{t}^{2}}{R}$
答:(1)t时该导体棒中的电流为$\frac{BLat}{R}$
(2)t时刻导体棒中水平向右的拉力为ma+$\frac{{B}^{2}{L}^{2}at}{R}$;
(3)t时刻回路的电功率为$\frac{{B}^{2}{L}^{2}{a}^{2}{t}^{2}}{R}$.
点评 此题中导体棒做匀加速直线运动,由运动学公式求出速度和位移,由E=BLv、I=$\frac{E}{R}$结合求解感应电流,再求电功率.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.1827年,第一个双星系统的完整轨道大熊座Xi由Felix Savary计算完成.两颗靠得很近的天体组合为双星,它们以两者连线上的某点为圆心,做匀速圆周运动,以下说法正确的是( )
| A. | 质量大的星体所需的向心力大 | |
| B. | 它们做圆周运动的线速度大小相等 | |
| C. | 它们的轨道半径与他们的质量成反比 | |
| D. | 它们的轨道半径与他们的质量的平方成反比 |
20.一多用电表的电阻档有三个倍率,分别是×1、×10、×100.用×10档测量某电阻时,操作步骤正确,发现表头指针偏转角度很小,为了较准确进行测量,正确的做法是( )
| A. | 为了使测量值比较准确,应该用两手分别将两表与待测电阻两端紧紧捏在一起,使表与待测电阻接触良好 | |
| B. | 这个电阻的阻值肯定也是极小的 | |
| C. | 应把选择开关换到×1档,将欧姆表重新调重零后进行调整 | |
| D. | 应将选择开关换到×100档,将欧姆表重新调重零后进行调整 |
17.发电厂发电机的输出电压为U1,发电厂至用户的输电导线的总电阻为R,通过输电导线的电流为I,用户两端得到的电压为U2,输电导线上损耗的功率可表示为( )
| A. | $\frac{{U}_{1}^{2}}{R}$ | B. | $\frac{{(U}_{1}-{U}_{2})^{2}}{R}$ | C. | I2R | D. | I(U1-U2) |
 如图所示,水平平行的固定光滑金属导轨MN、PQ相距L=0.5m,导轨左端用电阻R相连.水平导轨的某处有一竖直向上、磁感应强度B=0.2T的匀强磁场.质量m=0.2kg的金属杆ab以v0=5m/s的初速度沿水平导轨从左端冲入磁场,并以v=2m/s的速度离开磁场.设金属杆ab与轨道接触良好,并始终与导轨垂直.
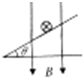
如图所示,水平平行的固定光滑金属导轨MN、PQ相距L=0.5m,导轨左端用电阻R相连.水平导轨的某处有一竖直向上、磁感应强度B=0.2T的匀强磁场.质量m=0.2kg的金属杆ab以v0=5m/s的初速度沿水平导轨从左端冲入磁场,并以v=2m/s的速度离开磁场.设金属杆ab与轨道接触良好,并始终与导轨垂直. 质量为m的通电细导杆ab置于倾角为θ的导轨上,导轨的宽度为d,杆ab与导轨间的摩擦因数为μ.有电流时,ab杆恰好在导轨上静止,如图(a)所示,图(b)中的四个侧视图中,标出了四种可能的匀强磁场方向,其中杆ab与导轨之间的摩擦力可能为零的图是( )
质量为m的通电细导杆ab置于倾角为θ的导轨上,导轨的宽度为d,杆ab与导轨间的摩擦因数为μ.有电流时,ab杆恰好在导轨上静止,如图(a)所示,图(b)中的四个侧视图中,标出了四种可能的匀强磁场方向,其中杆ab与导轨之间的摩擦力可能为零的图是( )