题目内容
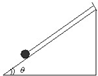 一个质量为0.2kg的小球用细线吊在倾角θ=53°的斜面顶端,如图,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s2的加速度向右做加速运动时,求绳的拉力及斜面对小球的弹力.
一个质量为0.2kg的小球用细线吊在倾角θ=53°的斜面顶端,如图,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s2的加速度向右做加速运动时,求绳的拉力及斜面对小球的弹力.分析:首先判断小球是否飞离了斜面,根据小球刚刚飞离斜面的临界条件,即绳子的倾角不变,斜面的支持力刚好为零,解出此时的加速度与题目给出的加速度大小进行比较,若给出加速度大于小球的临界加速度说明小球已经飞离了斜面,否则小球还在斜面上.
解答:解:当加速度a较小时,小球与斜面一起运动,此时小球受重力、绳子拉力和斜面的支持力,绳子平行于斜面;当加速度a足够大时,小球将飞离斜面,此时小球仅受重力与绳子的拉力作用,绳子与水平方向的夹角未知,而题目要求出当斜面以10m/s2的加速度向右做加速运动时,绳的拉力及斜面对小球的弹力,必须先求出小球离开斜面的临界加速度a0,(此时小球所受斜面的支持力恰好为零)
小球的受力如图:
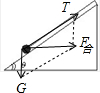
由牛顿第二定律得:F合=mgcotθ=ma0
解得:a0=gcotθ=7.5m/s2
因为:a=10m/s2>a0
所以小球一定离开斜面N=0,小球的受力如图所示:
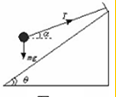
则水平方向有牛顿第二定律得:Tcosα=ma
竖直方向有受力平衡得:Tsinα=mg
由以上两式整理得:T=
=2.83N
N=0
答:绳的拉力为2.83N,斜面对小球的弹力为零.
小球的受力如图:

由牛顿第二定律得:F合=mgcotθ=ma0
解得:a0=gcotθ=7.5m/s2
因为:a=10m/s2>a0
所以小球一定离开斜面N=0,小球的受力如图所示:

则水平方向有牛顿第二定律得:Tcosα=ma
竖直方向有受力平衡得:Tsinα=mg
由以上两式整理得:T=
| (ma)2+(mg)2 |
N=0
答:绳的拉力为2.83N,斜面对小球的弹力为零.
点评:此题最难解决的问题是小球是否飞离了斜面,我们可以用假设法判断出临界加速度来进行比较.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个质量为0.2kg的弹性小球,在光滑水平面上以5m/s的速度垂直撞到墙上,碰撞后小球沿相反方向运动,
经0.1s反弹,反弹后的速度大小与碰撞前相同.则下列关于碰撞前后小球速度变化量的大小△v、碰撞过程中墙对小球做功的大小W、墙对小球的平均作用力大小F、动量变化量的大小△p的数值,正确的是( )
经0.1s反弹,反弹后的速度大小与碰撞前相同.则下列关于碰撞前后小球速度变化量的大小△v、碰撞过程中墙对小球做功的大小W、墙对小球的平均作用力大小F、动量变化量的大小△p的数值,正确的是( )
| A、△v=10m/s | B、W=10J | C、F=20N | D、△p=20kg?m/s |
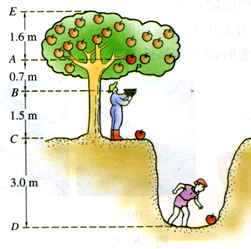 如图所示,一棵树上有一个质量为0.2kg的熟透了的苹果P,该苹果有可能被一个人用篮子在与B等高处接住,也可以落到地面C,还可能落到地面后滚入沟底D.(各点间的距离如图所示,忽略空气阻力的影响)
如图所示,一棵树上有一个质量为0.2kg的熟透了的苹果P,该苹果有可能被一个人用篮子在与B等高处接住,也可以落到地面C,还可能落到地面后滚入沟底D.(各点间的距离如图所示,忽略空气阻力的影响)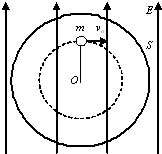 在光滑水平面上固定一个竖直圆筒S,圆筒内壁光滑(如图所示为俯视图),半径为1m.圆筒圆心O处用一根不可伸长的长0.5m的绝缘细线系住一个质量为0.2kg,电量为+5×10-5C的小球,小球体积忽略不计.水平方向有一匀强电场E=4×104N/C,方向如图所示.小球从图示位置(细线和电场线平行)以vo=10m/s垂直于场强方向运动.当细线转过900时,细线突然断裂.求:
在光滑水平面上固定一个竖直圆筒S,圆筒内壁光滑(如图所示为俯视图),半径为1m.圆筒圆心O处用一根不可伸长的长0.5m的绝缘细线系住一个质量为0.2kg,电量为+5×10-5C的小球,小球体积忽略不计.水平方向有一匀强电场E=4×104N/C,方向如图所示.小球从图示位置(细线和电场线平行)以vo=10m/s垂直于场强方向运动.当细线转过900时,细线突然断裂.求: