题目内容
12.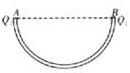 如图所示,在水平面上固定一个半圆形光滑的细管,在直径两端A、B分别放置一个正点电荷Q1、Q2,且Q2=8Q1.AB的距离为L,现将另一带正电的小球(可视为点电荷)从管内靠近A处由静止释放,设该点电荷沿细管运动到B过程中,以下说法正确的是( )
如图所示,在水平面上固定一个半圆形光滑的细管,在直径两端A、B分别放置一个正点电荷Q1、Q2,且Q2=8Q1.AB的距离为L,现将另一带正电的小球(可视为点电荷)从管内靠近A处由静止释放,设该点电荷沿细管运动到B过程中,以下说法正确的是( )| A. | 小球的速度先增加后减小 | |
| B. | 电势能最低的点与A点距$\frac{2\sqrt{5}}{5}$L | |
| C. | 电势能最低的点与B点相距$\frac{2\sqrt{5}}{5}$L | |
| D. | 对调Q1、Q2,电势能最低点的位置不变 |
分析 题目没有出现小球的质量,所以可以认为小球的重力不计,小球受到支持力和管子的支持力,在细管内运动,当受到的电场力的合力与细管垂直时,速度最大,结合库仑定律求出该点,然后依此解答即可.
解答 解:由电荷之间的相互作用的特点可知,正电荷受到A、B两处的正电荷的排斥力,当合力的方向沿半径的方向时,设该点为C点,BC与AB之间的夹角为θ,设小球的带电量 为q则:
为q则:
AC=Lsinθ,BC=L•cosθ,AC⊥BC
由库仑定律:${F}_{1}=\frac{kq{Q}_{1}}{{\overline{AC}}^{2}}$;${F}_{2}=\frac{kq{Q}_{2}}{{\overline{BC}}^{2}}$
当受到的电场力的合力与细管垂直时,由几何关系可得:
F1cosθ=F2sinθ
联立以上方程,解得:$tanθ=\frac{1}{2}$
A、由以上的分析可知,在C点与A点之间,A对小球的作用力沿细管的切线方向的分力比较大,所以小球做加速运动,而小球在C以下,B对小球的电场力沿切线方向的分力比较大,小球做减速运动.所以小球在AC之间做加速运动,过C点后做减速运动.故A正确;
B、C、小球在C点的速度最大,则但最小.由于$tanθ=\frac{1}{2}$,则sinθ=$\frac{\sqrt{5}}{5}$,cosθ=$\frac{2\sqrt{5}}{5}$,所以C点到A的距离为$\frac{\sqrt{5}}{5}$L,C点到B点的距离为$\frac{2\sqrt{5}}{5}$L.故B错误,C正确.
D、对调Q1、Q2,电势能最低点的位置仍然距离A比较近,位置将发生变化.故D错误.
故选:AC
点评 本题属于电场的叠加的题目类型,解答的关键是正确找出小球的速度最大的点,然后再结合题目的要求解答.

 阅读快车系列答案
阅读快车系列答案 如图所示,在水平面上放置的相距为0.2m的平行金属导轨与电源、电键、导体棒AB、滑动变阻器可构成闭合电路,磁感应强度为B=0.5T的匀强磁场竖直向下,导体棒AB的质量m=0.5kg,它与轨道之间的动摩擦因数μ=0.05.当电键S闭合时,电路中电流为5A(g取10m/s2).求:
如图所示,在水平面上放置的相距为0.2m的平行金属导轨与电源、电键、导体棒AB、滑动变阻器可构成闭合电路,磁感应强度为B=0.5T的匀强磁场竖直向下,导体棒AB的质量m=0.5kg,它与轨道之间的动摩擦因数μ=0.05.当电键S闭合时,电路中电流为5A(g取10m/s2).求: 在利用自由落体运动验证机械能守恒定律的实验中:
在利用自由落体运动验证机械能守恒定律的实验中:

 如图所示,位于竖直平面内的轨道,由一段斜的直轨道AB和光滑半圆形轨道BC平滑连接而成,AB的倾角为30°,半圆形轨道的半径.R=0.1m,直径BC竖直.质量m=1kg的小物块从斜轨道上距半圆形轨道底部高为h处由静止开始下滑,经B点滑上半圆形轨道.己知物块与斜轨道间的动摩擦因数为$\frac{\sqrt{3}}{6}$,g取g=10m/s2.
如图所示,位于竖直平面内的轨道,由一段斜的直轨道AB和光滑半圆形轨道BC平滑连接而成,AB的倾角为30°,半圆形轨道的半径.R=0.1m,直径BC竖直.质量m=1kg的小物块从斜轨道上距半圆形轨道底部高为h处由静止开始下滑,经B点滑上半圆形轨道.己知物块与斜轨道间的动摩擦因数为$\frac{\sqrt{3}}{6}$,g取g=10m/s2.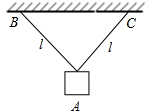
 如图所示,用恒力F将质量为m的物体从地面竖直向上提升高度为h,力F对物体做功为w1,用同样的恒力F将质量为2m的物体从地面竖直向上提升高度为h,力F对物体做功为w2,则w1:w2等于( )
如图所示,用恒力F将质量为m的物体从地面竖直向上提升高度为h,力F对物体做功为w1,用同样的恒力F将质量为2m的物体从地面竖直向上提升高度为h,力F对物体做功为w2,则w1:w2等于( )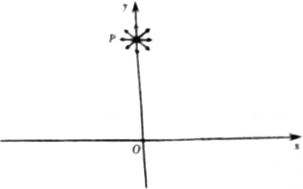 如图所示坐标系中,y轴上距原点O为d的P点有一个发射源,能够在纸面内向各个方向发射速率均为v0,质量为m,电量为q的带正电的小球,不考虑小球间的相互作用及空气阻力.
如图所示坐标系中,y轴上距原点O为d的P点有一个发射源,能够在纸面内向各个方向发射速率均为v0,质量为m,电量为q的带正电的小球,不考虑小球间的相互作用及空气阻力.