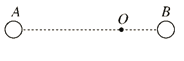题目内容
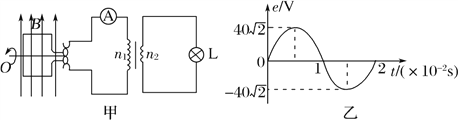
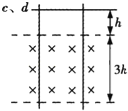
【题目】如图所示,两固定的竖直光滑金属导轨足够长且电阻不计.两质量、长度均相同的导体棒c、d,置于边界水平的匀强磁场上方同一高度h处.磁场宽为3h,方向与导轨平面垂直.先由静止释放c,c刚进入磁场即匀速运动,此时再由静止释放d,两导体棒与导轨始终保持良好接触.用ac表示c的加速度,Ekd表示d的动能,xc、xd分别表示c、d相对释放点的位移.选项中正确的是( )
A. 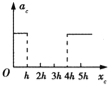 B.
B. 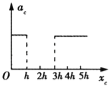 C.
C. 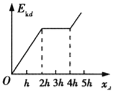 D.
D. 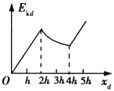
【答案】BD
【解析】试题分析:先释放c时,受重力加速度g是不变的,当c进入磁场时即做匀速运动,加速度为0,当d释放时,d的速度为0,然后d做匀加速,到它进入磁场时通过的距离为h,则c做一直匀速运动,c通过的距离为2h,二者一起又进入磁场,磁通量不变,回路中感应电流为0,安培力为0,故两棒做加速度为g的加速运动,故选项B正确,A错误;d棒的动能在d进入磁场前是均匀增加的,进入磁场后在c没有出磁场前也是均匀增加的,当c出磁场时,d棒切割磁感线,产生的安培力方向向上,阻碍d向下运动,但此时d的速度比刚进入磁场时的速度会大一些,所以棒不再像c刚开入那样做匀速运动,而是做减速运动,故选项C错误,D正确;待d棒完全出磁场后,它的加速度又是g,动能又能均匀增加了。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目