题目内容
8.如图甲所示,间距为d垂直于纸面的两平行板P、Q间存在匀强磁场,两板长均为L,取垂直于纸面向里为磁场的正方向,磁感应强度随时间的变化规律如图乙所示,一比荷为$\frac{q}{m}$=5πC/kg的带正电粒子(不计重力),t=0时刻以初速度v0由Q板左端靠近板面的位置,沿垂直于磁场且平行于板面的方向水平向右射入磁场区.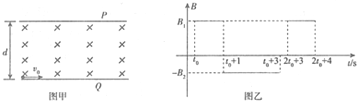
(1)t=(t0+1)s时,粒子速度首次变为水平向左,则B1多大?
(2)满足(1)的条件下,若B2=$\frac{1}{2}$B1,t0=$\frac{2}{π}$s,要使粒子速度水平向右到达P板的右端,求板长L的最小值和最大值,若板长L与板间距离d的比值为k,试求该比值的取值范围△k的最大值.
分析 (1)t0时刻起粒子做匀速圆周运动,经过半个圆周速度第一次变为水平向左,结合周期公式求出磁感应强度的大小.
(2)电场力和重力平衡,粒子在磁场中做圆周运动,根据半径公式求出粒子在不同磁场中做圆周运动的半径,要使粒子能平行向右到达A板右边沿,则粒子在两种磁场中回旋半周的次数相同,结合几何关系进行求解
解答 解:(1)t0时刻起粒子做匀速圆周运动,经过半个圆周速度第一次变为水平向左,设粒子在磁感应强度为B1的磁场中运动周期为T1,设粒子质量为m,电荷量为q,
有:T1=$\frac{2πm}{qB}$,且$\frac{1}{2}$T1=1s
解得:B1=0.2T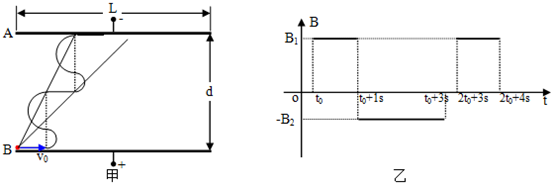
(2)设磁感应强度为B1和B2时粒子运动的半径分别为R1和R2,
有:R1=$\frac{m{v}_{0}}{q{B}_{1}}$=$\frac{{V}_{0}}{π}$,R2=$\frac{m{V}_{0}}{q{B}_{2}}$=$\frac{2{V}_{0}}{π}$,
要使粒子能平行向右到达A板右边沿,则粒子在两种磁场中回旋半周的次数相同,设为n,有:
d=2n(R1+R2)=$\frac{6n{V}_{0}}{π}$,
Lmin=nv0t0=$\frac{2n{V}_{0}}{π}$,
Lmax=(n+1)v0t0=$\frac{2(n+1){V}_{0}}{π}$(n=1,2,3,…)
kmax=$\frac{2n({R}_{1}+{R}_{2})}{n{V}_{0}{t}_{0}}$=3,
kmin=$\frac{2n({R}_{1}+{R}_{2})}{(n+1){V}_{0}{t}_{0}}$=$\frac{3n}{n+1}$,(n=1,2,3,…)
△k=kmax-kmin=$\frac{3}{n+1}$,当n=1 时,△k有最大值,且最大值为:△kmax=1.5.
答:(1)B1的大小为0.2T;
(2)比值的取值范围△k的最大值为1.5.
点评 本题考查了带电粒子在复合场中的运动,知道电场力和重力平衡,受洛伦兹力提供向心力,做圆周运动,结合半径公式、周期公式进行求解,第三问对数学能力要求较高,属于压轴部分,需加强这方面的训练

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 只要闭合电路内有磁通量,闭合电路中就有感应电流产生 | |
| B. | 穿过螺线管的磁通量变化时,螺线管内部就一定有感应电流产生 | |
| C. | 线框不闭合时,即使穿过线框的磁通量变化,线框内也没有感应电流 | |
| D. | 只要电路的一部分作切割磁感线运动,电路中就一定有感应电流 |
| A. | “神舟星”的轨道半径大 | B. | “神舟星”的公转周期大 | ||
| C. | “神舟星”受到的向心力大 | D. | “神舟星”的加速度大 |
| A. | α粒子散射实验是卢瑟福建立原子核式结构模型的重要依据 | |
| B. | 光电效应和康普顿效应深入揭示了光的粒子性,前者表明光子具有能量,后者表明光子除了具有能量外还具有动量 | |
| C. | 根据玻尔理论可知,氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动速度减小 | |
| D. | 在核反应中元素的种类不会改变 | |
| E. | ${\;}_{83}^{210}$Bi的半衰期是5天,12g${\;}_{83}^{210}$Bi经过15天后还有1.5g未衰变 |
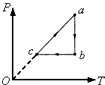
| A. | a→b过程中,气体体积减小,压强减小 | |
| B. | b→c过程中,气体压强不变,体积减小 | |
| C. | c→a过程中,气体内能增大,体积不变 | |
| D. | c→a过程中,气体压强增大,体积变小 |
| A. | 物体可能受空气阻力作用 | |
| B. | 物体的加速度可能大于g | |
| C. | 物体的加速度一定等于g | |
| D. | 经过较长时间后,物体的速度可能变为竖直向下 |
 如图所示,把一个质量m=0.2kg的小球从h=7.2m的高处以60°角斜向上抛出,初速度v0=5m/s,不计空气阻力,重力加速度g=10m/s2.问:
如图所示,把一个质量m=0.2kg的小球从h=7.2m的高处以60°角斜向上抛出,初速度v0=5m/s,不计空气阻力,重力加速度g=10m/s2.问: