题目内容
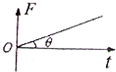如图a所示，固定在水平面内的光滑金属框架cdeg处于方向竖直向下的匀强磁场中，金属杆ab与金属框架接触良好．在两根导轨的端点d、e之间连接一电阻，其它部分电阻忽略不计．现用一水平向右的外力F作用在金属杆ab上，使金属杆在框架上由静止开始向右滑动，运动中杆ab始终垂直于框架．图b为一段时间内金属杆受到安培力f随时间t的变化关系，则图c中可以表示此段时间内外力F随时间t变化关系的图象是（ ）A、 | B、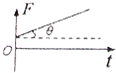 | C、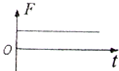 | D、 |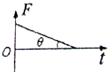
分析：金属杆由静止开始向右在框架上滑动时，水平方向受到外力F和安培力作用，可推导出安培力与速度的关系式，由图分析安培力随时间的变化情况，得到速度与时间的变化情况，根据牛顿第二定律，分析F与时间的关系．
解答：解：由感应电动势E=Blv，电流I=
得：
安培力为：f=BIl=
由图f∝t，则v∝t，说明导体做匀加速运动，那么v=at
根据牛顿第二定律，得：F-f=ma
得到：F=f+ma=
+ma．故B正确，A、C、D错误．
故选：B．
| E |
| R |
安培力为：f=BIl=
| B2l2v |
| R |
由图f∝t，则v∝t，说明导体做匀加速运动，那么v=at
根据牛顿第二定律，得：F-f=ma
得到：F=f+ma=
| B2l2at |
| R |
故选：B．
点评：本题由电磁感应知识和牛顿定律结合，得到F的解析式选择图象，这是常用方法．关键是安培力的分析和计算．
练习册系列答案
相关题目
某同学设计了如图a所示的装置来探究加速度与力的关系．轻质弹簧秤固定在一合适的木块上，桌面的右边缘固定一个光滑的定滑轮，细绳的两端分别与弹簧秤的挂钩和矿泉水瓶连接．在桌面上做标记P、Q，并测出间距为d．开始时将木块置于P处，现缓慢向瓶中加水，直到木块刚刚开始运动为止，记下弹簧秤的示数F，然后释放木块，并用数字计时器记下木块从P运动到Q处的时间为t．
