Question

已知某船在静水中的速率为4m/s，现让船渡过某条河，假设这条河的两岸是理想的平行线，河宽为100米，河水的流动速率为5m/s，方向与河岸平行，则（　　）

A．船不能垂直河岸渡河

B．欲使船渡过河去的航程最短，船头指向为斜向上游，与河岸成θ角，cosθ=0.8

C．最短航程是125米

D．船能垂直河岸渡河，最短航程是100米

Answer 1

分析：通过合速度的方向能否垂直于河岸，确定船能否垂直渡河．当合速度的方向与静水速的方向垂直时，渡河的航程最短，根据平行四边形定则求出船头的指向，以及最短航程．

解答：解：A、因为静水速小于水流速，所以合速度不可能垂直于河岸，则船不能垂直河岸渡河．故A正确，D错误．
B、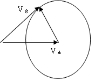当合速度的方向与静水速的方向垂直时，渡河航程最短，如图所示，则cosθ=

v静

v水

=0.8．渡河的最短航程s=

d

cosθ

=

100

0.8

m=125m．故B、C正确．
故选ABC．

点评：解决本题的关键当静水速大于水流速，合速度与河岸垂直，渡河航程最短，当静水速小于水流速，合速度与静水速垂直，渡河航程最短．