题目内容
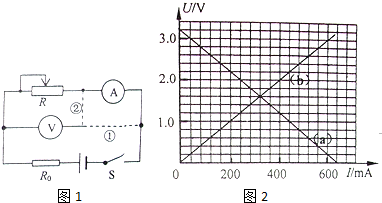
如图1-10(a)所示,光滑的平行长直金属导轨置于水平面内,间距为L.导轨左端接有阻值为R的电阻,质量为m的导体棒垂直跨接在导轨上.导轨和导体棒的电阻均不计,且接触良好.在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为B.开始时,导体棒静止于磁场区域的右端,当磁场以速度v1匀速向右移动时,导体棒随之开始运动,同时受到水平向左、大小为f的恒定阻力,并很快达到恒定速度,此时导体棒仍处于磁场区域内.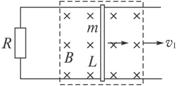
(a) (b)
图1-10
(1)求导体棒所达到的恒定速度v2;
(2)为使导体棒能随磁场运动,阻力最大不能超过多少?
(3)导体棒以恒定速度运动时,单位时间内克服阻力所做的功和电路中消耗的电功率各为多大?
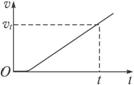
(4)若t=0时磁场由静止开始水平向右做匀加速直线运动,经过较短时间后,导体棒也做匀加速直线运动,其v-t关系如图1-10(b)所示.已知在时刻t导体棒的瞬时速度大小为vt,求导体棒做匀加速直线运动时的加速度大小.
解析:(1)磁场以恒定速度v1向右移动(若导体棒不动),电阻、导体棒和导轨构成的回路内磁场区域的面积变小![]() =Lv1
=Lv1
导体棒以恒定速度v2向右移动,回路面积变大
![]() =Lv2
=Lv2
两者一起运动,回路中磁场区域的面积变小
![]() =L(v1-v2)
=L(v1-v2)
回路中磁通量变化,产生电动势和电流
ε=![]() =B
=B![]() =BL(v1-v2)
=BL(v1-v2)
I=![]() (v1-v2)
(v1-v2)
导体棒匀速运动,安培力与阻力相等
F安=IBL=![]() (v1-v2)=f ①
(v1-v2)=f ①
所以v2=![]() . ②
. ②
(2)由②式,f越大,v2越小,v2最小为0
所以fm=![]() v1.
v1.
(3)设导体棒以恒定速度v2运动
P导体棒=fv2,以②结果代入,得
P导体棒=f(![]() )
)
P电路=I2R=![]() (v1-v2)2,以①、②结果代入,得
(v1-v2)2,以①、②结果代入,得
P电路=f(v1-v2)=![]() .
.
(4)设磁场的加速度为a,金属棒的加速度为a′,当金属棒以一定速度v运动时,受安培力和阻力作用,由牛顿第二定律![]() (at-v)-f=ma′
(at-v)-f=ma′
由图可知,在t时刻导体棒的瞬时速度大小为vt,此时棒做匀加速运动,磁场与棒之间速度差为恒量,因此必有a=a′,即
![]() (at-vt)-f=ma,所以a′=a=
(at-vt)-f=ma,所以a′=a=![]() .
.
答案:(1)![]() (2)
(2)![]()
(3)f(![]() )
) ![]() (4)
(4)![]()

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 (1)在“验证力的平行四边形法则”实验中,某同学的实验结果如图1,其中A为固定橡皮条的图钉,O为橡皮条与细绳结点的位置.图中
(1)在“验证力的平行四边形法则”实验中,某同学的实验结果如图1,其中A为固定橡皮条的图钉,O为橡皮条与细绳结点的位置.图中