题目内容
17. 质量为m=2.0×10-11kg,电荷量为q=1.0×10-5C的带负电粒子自静止开始,经M、N板间的电场加速后,从A点垂直于磁场边界射入宽度为d=10cm的匀强磁场中,该粒子恰好不离开磁场右边界(在磁场右边界粒子速度与边界平行),如图所示.已知M、N两板间的电压为U=100V,粒子的重力不计.
质量为m=2.0×10-11kg,电荷量为q=1.0×10-5C的带负电粒子自静止开始,经M、N板间的电场加速后,从A点垂直于磁场边界射入宽度为d=10cm的匀强磁场中,该粒子恰好不离开磁场右边界(在磁场右边界粒子速度与边界平行),如图所示.已知M、N两板间的电压为U=100V,粒子的重力不计.(1)求出粒子进入匀强磁场时的速度大小
(2)在磁场中画出运动轨迹,求出半径为r
(3)求匀强磁场的磁感应强度B的大小.
分析 (1)带电粒子在电场中加速,由动能定理可以求出粒子进入磁场时的速度.
(2)根据几何关系求出粒子在磁场中的半径.
(3)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出磁感应强度.
解答 解:(1)带电粒子在M、N间加速后获得的速度为v,由动能定理得:$\frac{1}{2}$mv2-0=qU
代入数据得:v=104 m/s
(2)粒子恰好不离开磁场右边界,如图;由几何关系可得:r=d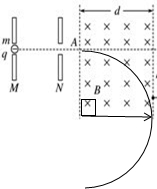
(3)洛仑兹力提供向心力qvB=$\frac{m{v}^{2}}{r}$
联立可得:B=$\frac{mv}{qr}=\frac{mv}{qd}=\frac{2.0×1{0}^{-11}×1{0}^{4}}{1×1{0}^{-5}×0.1}=0.2$T
答:(1)带电粒子进入磁场时的速度是104 m/s.
(2)带电粒子在磁场中运动的轨道半径r为$\frac{{d}^{2}+{L}^{2}}{2L}$d
(3)匀强磁场的磁感应强度B为0.2T.
点评 电子垂直于磁场方向射入磁场后做匀速圆周运动,洛伦兹力提供向心力;由几何知识求出电子轨道半径是求出磁感应强度的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
2. 如图所示,A、B两物体叠放,水平力F作用在A上,使两者一起向右做匀速直线运动.下列判断中正确的是( )
如图所示,A、B两物体叠放,水平力F作用在A上,使两者一起向右做匀速直线运动.下列判断中正确的是( )
 如图所示,A、B两物体叠放,水平力F作用在A上,使两者一起向右做匀速直线运动.下列判断中正确的是( )
如图所示,A、B两物体叠放,水平力F作用在A上,使两者一起向右做匀速直线运动.下列判断中正确的是( )| A. | 由于A、B一起做匀速直线运动,故A、B之间无摩擦力 | |
| B. | A对B的摩擦力大小为F,方向向右 | |
| C. | B对地面的滑动摩擦力的大小为F,方向向右 | |
| D. | B物体受到的静摩擦力和滑动摩擦力的方向都向左 |
6.设在平直的公路上以一般速度行驶的自行车,所受的阻力约为人、车总重力的0.02倍,则骑车人的功率与下述数值最接近的是( )
| A. | 10KW | B. | 1KW | C. | 100W | D. | 10-3KW |


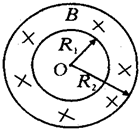 据有关资料介绍,受控热核聚变反应装置中有极高的温度,因而带电粒子将没有通常意义上的容器可装,而是由磁场约束带电粒子运动将其束缚在某个区域内,现按下面的简化条件来讨论这个问题,如图所示,有一个环形区域,其截面内半径为R1=$\frac{\sqrt{3}}{3}$m,外半径为R2=1.0m,区域内有垂直纸面向里的匀强磁场,已知磁感应强度B=1.0T,被束缚粒子的荷质比为$\frac{q}{m}$=4.0×107C/kg,不计带电粒子在运动过程中的相互作用,不计带电粒子的重力.
据有关资料介绍,受控热核聚变反应装置中有极高的温度,因而带电粒子将没有通常意义上的容器可装,而是由磁场约束带电粒子运动将其束缚在某个区域内,现按下面的简化条件来讨论这个问题,如图所示,有一个环形区域,其截面内半径为R1=$\frac{\sqrt{3}}{3}$m,外半径为R2=1.0m,区域内有垂直纸面向里的匀强磁场,已知磁感应强度B=1.0T,被束缚粒子的荷质比为$\frac{q}{m}$=4.0×107C/kg,不计带电粒子在运动过程中的相互作用,不计带电粒子的重力. 有一10匝正方形线框,边长为20cm,线框总电阻为1Ω,线框OO′轴以10πrad/s的角速度匀速转动,如图所示,垂直于线框平面向里的匀强磁场磁感应强度为0.5T,问:
有一10匝正方形线框,边长为20cm,线框总电阻为1Ω,线框OO′轴以10πrad/s的角速度匀速转动,如图所示,垂直于线框平面向里的匀强磁场磁感应强度为0.5T,问: