题目内容
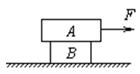
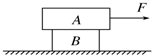如图所示，长方体物块A叠放在长方体物块B上，B置于光滑水平面上．A、B质量分别为mA=6kg，mB=2kg，A、B之间动摩擦因数μ=0.2，开始时F=10N，此后逐渐增加，在增大到45N的过程中，则（ ）| A、当拉力F＜12N时，两物块均保持静止状态 | B、两物块间从受力开始就有相对运动 | C、两物块开始没有相对运动，当拉力超过12N时，开始相对滑动 | D、两物块间始终没有相对运动，但AB间存在静摩擦力，其中A对B的静摩擦力平向右 |
分析：隔离对B分析，求出AB发生相对滑动时的临界加速度，再对整体分析，运用牛顿第二定律求出刚好发生相对滑动时的拉力．
解答：解：隔离对B分析，当AB间摩擦力达到最大静摩擦力时，A、B发生相对滑动，则aB=
=
=6m/s2．
再对整体分析F=（mA+mB）a=8×6N=48N．知当拉力达到48N时，A、B才发生相对滑动．由于地面光滑，只要有拉力两物体就一起运动．
故选：D
| μmAg |
| mB |
| 0.2×6×10 |
| 2 |
再对整体分析F=（mA+mB）a=8×6N=48N．知当拉力达到48N时，A、B才发生相对滑动．由于地面光滑，只要有拉力两物体就一起运动．
故选：D
点评：本题考查牛顿第二定律的临界问题，关键找出临界状态，运用整体法和隔离法，根据牛顿第二定律进行求解．
练习册系列答案
阅读快车系列答案
相关题目
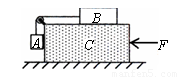
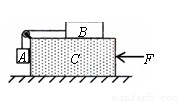
（2010?镇江一模）如图所示，长方体物块C置于水平地面上，物块A、B用不可伸长的轻质细绳通过滑轮连接（不计滑轮与绳之间的摩擦），A物块与C物块光滑接触，整个系统中的A、B、C三物块在水平恒定推力F作用下从静止开始以相同的加速度一起向左运动．下列说法正确的是（ ）
