题目内容
 频率不同的两束单色光1和2 以相同的入射角从同一点射入一厚平行玻璃板后,其光路如图所示,下列说法正确的是( )
频率不同的两束单色光1和2 以相同的入射角从同一点射入一厚平行玻璃板后,其光路如图所示,下列说法正确的是( )分析:由题可知,两束光在平行玻璃板上表面第一次折射时,入射角相同,1的折射角小于2的折射角,根据折射定律确定折射率的大小.由sinC=
分析临界角的大小.由公式v=
分析两束光在玻璃砖中速度关系.由几何知识研究光在玻璃砖中路程关系,分析时间关系.干涉干涉条纹宽度与波长成正比.1的波长小于2的波长,单色光1的干涉条纹宽度小于单色光2干涉条纹宽度.
| 1 |
| n |
| c |
| n |
解答:解:A、两束光在平行玻璃板上表面第一次折射时,入射角相同,1的折射角小于2的折射角,根据折射定律可知,下玻璃对单色光1的折射率大于对单色光1的折射率,即n1>n2.由sinC=
分析可知,单色光1从玻璃到空气的全反射临界角小于单色光2从玻璃到空气的全反射临界角.故A正确.
B、由公式v=
分析得出,在玻璃中单色光1的传播速度小于单色光2的传播速度.故B错误.
C、设任一光线入射角为i,折射角r,玻璃砖厚度为d,则
光在玻璃砖中传播时间t=
=
又由折射定律得
n=
代入得 t=
,由上知道,n1>n2,而d、c、i均相同,则得到t1>t2.故C错误.
D、在相同条件下,单色光1的干涉条纹宽度小于单色光2干涉条纹宽度.故D正确.
故选AD
| 1 |
| n |
B、由公式v=
| c |
| n |
C、设任一光线入射角为i,折射角r,玻璃砖厚度为d,则
光在玻璃砖中传播时间t=
| ||
| v |
| dn | ||
c
|
又由折射定律得
n=
| sini |
| sinr |
代入得 t=
| d | ||||||
c
|
D、在相同条件下,单色光1的干涉条纹宽度小于单色光2干涉条纹宽度.故D正确.
故选AD
点评:本题重点考查光的折射率、频率、速度、波长和临界角等的概念和公式,加强这部分内容的反复记忆是不失分的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 频率不同的两束单色光1和2 以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示,已知玻璃板对这两束光的折射率均大于
频率不同的两束单色光1和2 以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示,已知玻璃板对这两束光的折射率均大于| 2 |
| A、在玻璃中单色光1的波长大于单色光2的波长 |
| B、单色光1通过玻璃板所需的时间小于单色光2通过玻璃板所需的时间 |
| C、单色光1通过玻璃板所需的时间大于单色光2通过玻璃板所需的时间 |
| D、单色光1从玻璃到空气的全反射临界角大于单色光2从玻璃到空气的全反射临界角 |
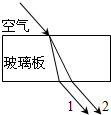 (2012?丰台区一模)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示.下列说法正确的是( )
(2012?丰台区一模)频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,其光路如图所示.下列说法正确的是( )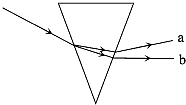 (2013?凉山州模拟)频率不同的两束单色光a和b以相同的入射角从同一点射入某玻璃棱镜后,光路如图所示,下列说法正确的是( )
(2013?凉山州模拟)频率不同的两束单色光a和b以相同的入射角从同一点射入某玻璃棱镜后,光路如图所示,下列说法正确的是( )