题目内容
如图所示,半圆形光滑绝缘轨道固定在竖直平面内,O为其圆心,两个端点M、N与O等高,匀强磁场方向与轨道平面垂直。现将一个带负电的小球自M点由静止释放,它将沿轨道做往复运动,下列说法中不正确的是:( )
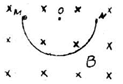

| A.小球由M到N与由 N到M所用时间相等 |
| B.小球由M到N与由N到M过程中重力对小球做的功相等。 |
| C.小球经过轨道最低点时所受合外力大小总是完全相同的 |
| D.小球经过轨道最低点时对轨道的压力大小总是相等的 |
D
因为小球运动过程中只有重力做功,洛伦兹力不国公,所以小球从M到N与从N到M过程中重力对小球做的功相等都为零。运动时间相同,所以AB正确。到最低点时两种情况下小球下落高度相等,所以根据动能定理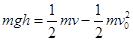 可得小球在最低点的速度是相等的,根据牛顿第二定律可得
可得小球在最低点的速度是相等的,根据牛顿第二定律可得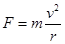 ,即在两种情况在最低点的向心力大小相等即合力大小相等,C正确。在从M到N的过程中最低点小球受到的洛伦兹力方向竖直向下,故有
,即在两种情况在最低点的向心力大小相等即合力大小相等,C正确。在从M到N的过程中最低点小球受到的洛伦兹力方向竖直向下,故有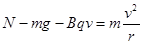 ,从N点到M点的过程中的最低点小球受到的洛伦兹力方向竖直向上,故有
,从N点到M点的过程中的最低点小球受到的洛伦兹力方向竖直向上,故有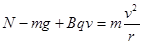 ,所以两种情况下小球经过最低点时对轨道的压力大小是不相同的,D错误。
,所以两种情况下小球经过最低点时对轨道的压力大小是不相同的,D错误。
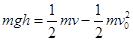 可得小球在最低点的速度是相等的,根据牛顿第二定律可得
可得小球在最低点的速度是相等的,根据牛顿第二定律可得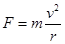 ,即在两种情况在最低点的向心力大小相等即合力大小相等,C正确。在从M到N的过程中最低点小球受到的洛伦兹力方向竖直向下,故有
,即在两种情况在最低点的向心力大小相等即合力大小相等,C正确。在从M到N的过程中最低点小球受到的洛伦兹力方向竖直向下,故有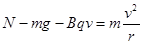 ,从N点到M点的过程中的最低点小球受到的洛伦兹力方向竖直向上,故有
,从N点到M点的过程中的最低点小球受到的洛伦兹力方向竖直向上,故有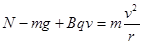 ,所以两种情况下小球经过最低点时对轨道的压力大小是不相同的,D错误。
,所以两种情况下小球经过最低点时对轨道的压力大小是不相同的,D错误。
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目