题目内容
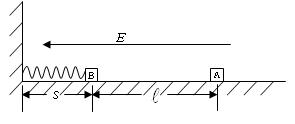
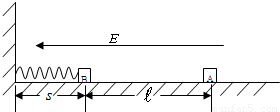
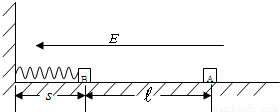
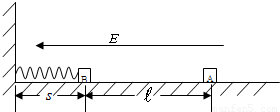
在绝缘水平面上,放一质量为m=2.0×10-3kg的带正电滑块A,所带电量为q=1.0×10-7C,在滑块A的左边?处放置一个不带电、质量M=4.0×10-3kg的绝缘滑块B,B的左端接触(不连接)于固定在竖直墙壁的轻弹簧上,轻弹簧处于自然状态,弹簧原长s=0.05m,如图所示.在水平方向加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后结合在一起共同运动的速度为v=1m/s,两物体一起压缩弹簧至最短处(弹性限度内)时,弹簧的弹性势能E=3.2×10-3J.设两滑块体积大小不计,与水平面间的动摩擦因数为μ=0.50,摩擦不起电,碰撞不失电,g取10m/s2.求:(1)两滑块在碰撞前的瞬时,滑块A的速度;
(2)滑块A起始运动位置与滑块B的距离?;
(3)B滑块被弹簧弹开后距竖起墙的最大距离sm.
【答案】分析:(1)A、B两滑块碰撞过程动量守恒,已知碰后的共同速度,根据动量守恒定律即可求得碰前A的速度.
(2)对于碰前A向左匀加速运动过程,运用动能定理可求出l.
(3)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理即可求得弹簧压缩量,弹簧压缩过程中电场力做正功,电势能的减少量等于电场力所做的功;设反弹后A、B滑行了x2距离后速度减为零,由动能定理求得x2,比较电场力与滑动摩擦力的关系,判断滑块的运动情况,最终求出最大距离.
解答:解:(1)设A与B碰撞前A的速度为v1,碰撞过程动量守恒,有:
mv1=(M+m)v
代入数据解得:v1=3m/s
(2)对A,从开始运动至碰撞B之前,根据动能定理,有:
qE?-μmg?=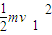 -0
-0
代入数据解得:?=0.3m
(3)设弹簧被压缩至最短时的压缩量为s1,对AB整体,从碰后至弹簧压缩最短过程中,根据能量守恒定律,有:
qEs1+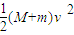 =μmg s1+E
=μmg s1+E
代入数据解得:s1=0.02m
设弹簧第一次恢复到原长时,AB共同动能为Ek,根据能量守恒定律,有:
E=qEs1+μ(M+m)g s1+Ek ①
在弹簧把BA往右推出的过程中,由于B受到向左的摩擦力小于A受到的向左的摩擦力和电场力之和.故至他们停止之前,两者没有分开.
弹簧第一次将AB弹出至两者同时同处停止时,B距离竖直墙壁最远,设此时距离弹簧原长处为s2,根据动能定理,有:
-qEs2-μ(M+m)g s2=0-Ek ②
①②联立并代入数据解得:s2=0.03m
故B离墙壁的最大距离sm=s+s2=0.08m
答:
(1)两滑块在碰撞前的瞬时,滑块A的速度为3m/s.
(2)滑块A起始运动位置与滑块B的距离?为0.3m.
(3)B滑块被弹簧弹开后距竖起墙的最大距离sm为0.08m.
点评:本题主要考查了动能定理和动量守恒定律的直接应用,要培养自己分析物理过程,把握物理规律,解决综合题的能力.
(2)对于碰前A向左匀加速运动过程,运用动能定理可求出l.
(3)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理即可求得弹簧压缩量,弹簧压缩过程中电场力做正功,电势能的减少量等于电场力所做的功;设反弹后A、B滑行了x2距离后速度减为零,由动能定理求得x2,比较电场力与滑动摩擦力的关系,判断滑块的运动情况,最终求出最大距离.
解答:解:(1)设A与B碰撞前A的速度为v1,碰撞过程动量守恒,有:
mv1=(M+m)v
代入数据解得:v1=3m/s
(2)对A,从开始运动至碰撞B之前,根据动能定理,有:
qE?-μmg?=
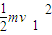 -0
-0代入数据解得:?=0.3m
(3)设弹簧被压缩至最短时的压缩量为s1,对AB整体,从碰后至弹簧压缩最短过程中,根据能量守恒定律,有:
qEs1+
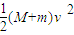 =μmg s1+E
=μmg s1+E 代入数据解得:s1=0.02m
设弹簧第一次恢复到原长时,AB共同动能为Ek,根据能量守恒定律,有:
E=qEs1+μ(M+m)g s1+Ek ①
在弹簧把BA往右推出的过程中,由于B受到向左的摩擦力小于A受到的向左的摩擦力和电场力之和.故至他们停止之前,两者没有分开.
弹簧第一次将AB弹出至两者同时同处停止时,B距离竖直墙壁最远,设此时距离弹簧原长处为s2,根据动能定理,有:
-qEs2-μ(M+m)g s2=0-Ek ②
①②联立并代入数据解得:s2=0.03m
故B离墙壁的最大距离sm=s+s2=0.08m
答:
(1)两滑块在碰撞前的瞬时,滑块A的速度为3m/s.
(2)滑块A起始运动位置与滑块B的距离?为0.3m.
(3)B滑块被弹簧弹开后距竖起墙的最大距离sm为0.08m.
点评:本题主要考查了动能定理和动量守恒定律的直接应用,要培养自己分析物理过程,把握物理规律,解决综合题的能力.

练习册系列答案
相关题目
 (2008?揭阳二模)在绝缘水平面上,放一质量为m=2.0×10-3kg的带正电滑块A,所带电量为q=1.0×10-7C,在滑块A的左边?处放置一个不带电、质量M=4.0×10-3kg的绝缘滑块B,B的左端接触(不连接)于固定在竖直墙壁的轻弹簧上,轻弹簧处于自然状态,弹簧原长s=0.05m,如图所示.在水平方向加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后结合在一起共同运动的速度为v=1m/s,两物体一起压缩弹簧至最短处(弹性限度内)时,弹簧的弹性势能E0=3.2×10-3J.设两滑块体积大小不计,与水平面间的动摩擦因数为μ=0.50,摩擦不起电,碰撞不失电,g取10m/s2.求:
(2008?揭阳二模)在绝缘水平面上,放一质量为m=2.0×10-3kg的带正电滑块A,所带电量为q=1.0×10-7C,在滑块A的左边?处放置一个不带电、质量M=4.0×10-3kg的绝缘滑块B,B的左端接触(不连接)于固定在竖直墙壁的轻弹簧上,轻弹簧处于自然状态,弹簧原长s=0.05m,如图所示.在水平方向加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后结合在一起共同运动的速度为v=1m/s,两物体一起压缩弹簧至最短处(弹性限度内)时,弹簧的弹性势能E0=3.2×10-3J.设两滑块体积大小不计,与水平面间的动摩擦因数为μ=0.50,摩擦不起电,碰撞不失电,g取10m/s2.求: