题目内容
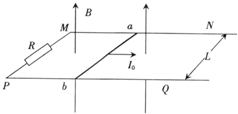 如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个初速度V0,使ab杆向右滑行.
如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个初速度V0,使ab杆向右滑行.(1)求回路的最大电流.
(2)当滑行过程中电阻上产生的热量为Q时,杆ab的加速度多大?
分析:(1)金属杆在导轨上做减速运动,刚开始时速度最大,由E=BLv和I=
结合求出最大电流.
(2)先由能量守恒求出杆ab的速度,再根据E=BLv,I=
和F=BIL推导出安培力表达式,由牛顿第二定律求解加速度.
| E |
| R |
(2)先由能量守恒求出杆ab的速度,再根据E=BLv,I=
| E |
| R |
解答:解:(1)由题,ab杆向右切割磁感线时产生感应电流,杆将受到安培力阻碍而做减速运动,速度减小,安培力大小随之减小,则加速度减小.故杆做加速度减小的减速运动直到停止运动.由上分析可知,金属杆在导轨上做减速运动,则刚开始时速度最大,感应电动势也最大,有:
Em=BLv0
所以回路的最大电流为:Im=
,金属杆上的电流方向从a到b.
(2)设此时杆的速度为v,由能量守恒有:Q=
mv02-
mv2 …①.
由牛顿第二定律得:FA=BIL=ma…②
闭合电路欧姆定律有:I=
…③
联立①②③得:a=
答:(1)回路的最大电流为
.
(2)当滑行过程中电阻上产生的热量为Q时,杆ab的加速度为
.
Em=BLv0
所以回路的最大电流为:Im=
| BLV0 |
| R |
(2)设此时杆的速度为v,由能量守恒有:Q=
| 1 |
| 2 |
| 1 |
| 2 |
由牛顿第二定律得:FA=BIL=ma…②
闭合电路欧姆定律有:I=
| BLv |
| R |
联立①②③得:a=
| B2L2 |
| mR |
|
答:(1)回路的最大电流为
| BLV0 |
| R |
(2)当滑行过程中电阻上产生的热量为Q时,杆ab的加速度为
| B2L2 |
| mR |
|
点评:本题通过杆的受力情况来分析其运动情况,关键要抓住安培力大小与速度大小成正比.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目




