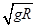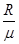题目内容
 有四分之一光滑圆弧轨道的小车总质量为M=3kg,静止在光滑的水平地面上,下端水平,光滑圆弧轨道的半径为R=0.5m,有一质量为m=1kg的物块以水平初速度v0=4m/s从A点滑上小车,取g=10m/s2求:
有四分之一光滑圆弧轨道的小车总质量为M=3kg,静止在光滑的水平地面上,下端水平,光滑圆弧轨道的半径为R=0.5m,有一质量为m=1kg的物块以水平初速度v0=4m/s从A点滑上小车,取g=10m/s2求:(1)物块运动到圆弧轨道最高点时,车的速度为多大?
(2)物块上升到最高点时,距B点的竖直高度为多少?
(3)小球离开车时,车的速度为多大?
分析:1、在光滑水平地面上,水平方向的合力为零,所以系统水平方向上动量守恒,列出等式求解
2、小球在最大高度时,竖直方向小球的速度为零,而水平方向上又不能越过小车,所以小球在最大高度时二者速度相等.根据能量守恒列出等式求解.
3、根据系统水平方向上动量守恒,列出等式求解.
2、小球在最大高度时,竖直方向小球的速度为零,而水平方向上又不能越过小车,所以小球在最大高度时二者速度相等.根据能量守恒列出等式求解.
3、根据系统水平方向上动量守恒,列出等式求解.
解答:解:(1)小球在最大高度时,竖直方向小球的速度为零,而水平方向上又不能越过小车,所以小球在最大高度时二者速度相等.
在光滑水平地面上,水平方向的合力为零,所以系统水平方向上动量守恒,列出等式
mv0=(M+m)v
v=1m/s
(2)小球从开始到最大高度时,对于系统,根据能量守恒列出等式:
mgh=
-
(M+m)v2
h=0.6m
所以物块上升到最高点时,距B点的竖直高度为0.6-0.5m=0.1m
(3)小球离开车时,设小球的速度大小v′,方向向右,
根据系统水平方向上动量守恒,规定向左为正方向,列出等式:
mv0=-mv′+Mv″
根据能量守恒得小球离开车时,
=
+
联立解得:v′=2m/s v″=2m/s
(1)物块运动到圆弧轨道最高点时,车的速度为1m/s
(2)物块上升到最高点时,距B点的竖直高度为0.1m
(3)小球离开车时,车的速度为2m/s
在光滑水平地面上,水平方向的合力为零,所以系统水平方向上动量守恒,列出等式
mv0=(M+m)v
v=1m/s
(2)小球从开始到最大高度时,对于系统,根据能量守恒列出等式:
mgh=
| 1 |
| 2 |
| mv | 2 0 |
| 1 |
| 2 |
h=0.6m
所以物块上升到最高点时,距B点的竖直高度为0.6-0.5m=0.1m
(3)小球离开车时,设小球的速度大小v′,方向向右,
根据系统水平方向上动量守恒,规定向左为正方向,列出等式:
mv0=-mv′+Mv″
根据能量守恒得小球离开车时,
| 1 |
| 2 |
| mv | 2 0 |
| 1 |
| 2 |
| mv′ | 2 |
| 1 |
| 2 |
| Mv″ | 2 |
联立解得:v′=2m/s v″=2m/s
(1)物块运动到圆弧轨道最高点时,车的速度为1m/s
(2)物块上升到最高点时,距B点的竖直高度为0.1m
(3)小球离开车时,车的速度为2m/s
点评:本题是系统水平方向动量守恒和能量守恒的问题,应用动量守恒时一定要注意方向问题.

练习册系列答案
相关题目
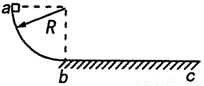
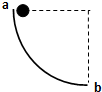 如图所示,将一质量为m的小球从竖直面内的四分之一光滑圆弧轨道的a点由静止释放,则小球到达圆弧轨道最低点b时对圆弧轨道的压力为( )
如图所示,将一质量为m的小球从竖直面内的四分之一光滑圆弧轨道的a点由静止释放,则小球到达圆弧轨道最低点b时对圆弧轨道的压力为( )| A、mg | B、2mg | C、3mg | D、4mg |
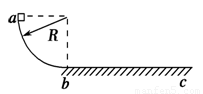
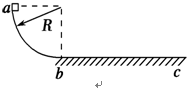 (2012?珠海一模)如图所示,在半径为R的四分之一光滑圆弧轨道的顶端a点,质量为 m 的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b 点与水平轨道平滑相接,物块最终滑至c 点停止.若物块与水平面间的动摩擦因数为μ,下列说法正确的是( )
(2012?珠海一模)如图所示,在半径为R的四分之一光滑圆弧轨道的顶端a点,质量为 m 的物块(可视为质点)由静止开始下滑,经圆弧最低点b滑上粗糙水平面,圆弧轨道在b 点与水平轨道平滑相接,物块最终滑至c 点停止.若物块与水平面间的动摩擦因数为μ,下列说法正确的是( )